Bài 13 trang 117 Vở bài tập toán 7 tập 1

Đề bài

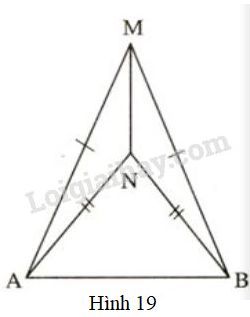
Xét bài toán: "\(\Delta AMB\) và \(\Delta ANB\) có \(MA=MB, NA=NB\) (h.71). Chứng minh rằng

\(\widehat{AMN}=\widehat{BMN}\)."

1) Hãy ghi giả thiết và kết luận của bài toán.

2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bài toán trên :

a) Do đó  \(\Delta AMN=\Delta BMN (c.c.c)\)

b)

\(MN\) cạnh chung

\(MA=MB\) (giả thiết)

\(NA= NB\) (giả thiết)

c) Suy ra \(\widehat{AMN}=\widehat{BMN}\) (hai góc tương ứng)

d) \(\Delta AMN\) và \(\Delta BMN\) có:

Lời giải chi tiết

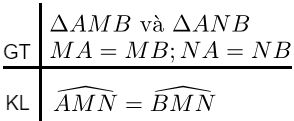
Thứ tự sắp xếp bốn câu trên là d, b, a, c như sau:

\(\Delta AMN\) và \(\Delta BMN\) có:

\(MN\) cạnh chung

\(MA=MB\) (giả thiết)

\(NA= NB\) (giả thiết)

Do đó  \(\Delta AMN=\Delta BMN (c.c.c)\)

Suy ra \(\widehat{AMN}=\widehat{BMN}\) (hai góc tương ứng).