Bài 1.1, 1.2, 1.3, 1.4 trang 3 SBT Vật Lí 12

1.1

Một vật dao động điều hòa có quỹ đạo là một đoạn thẳng dài 30cm. Biên độ dao động của vật là bao nhiêu ?

A. 30cm            B.15 cm        

C. -15 cm          D. 7,5 cm

Phương pháp giải:

Sử dụng biểu thức xác định chiều dài quỹ đạo chuyển động của vật \(L=2A\)

Giải chi tiết:

Quỹ đọa chuyển động của vật trong dao động điều hòa là \(2A\)

\(\begin{array}{l} \Rightarrow 2A = 30\\ \Leftrightarrow A = 15cm\end{array}\)

Chọn B

1.2

Tốc độ một vật dao động điều hòa cực đại khi nào ?

A. Khi t = 0          B. Khi t = \(\displaystyle{T \over 4}\)      

C. Khi t = \(\displaystyle{T \over 2}\)       D. Khi vật đi qua vị trí cân bằng

Phương pháp giải:

Lý thuyết về vận tốc chất điểm trong dao động điều hòa

Giải chi tiết:

Khi chất điểm đi qua vị trí cân bằng thì có tốc độ cực đại

Chọn D

1.3

Một điểm chuyển động tròn đều với tốc độ dài 0,60 m/s trên một đường tròn đường kính 0,40 m. Hình chiếu của nó lên một đường kính dao động điều hòa với biên độ, chu kì và tần số góc là:

A. 0,40 m; 2,1s ; 3rad/s        

B. 0,40 m; 4,8s ; 3,0 rad/s

C. 0,20 m; 4,2 s ; 1,5rad/s       

D. 0,20 m; 2,1 s ; 3,0 rad/s

Phương pháp giải:

Lý thuyết về mối liên hệ giữa dao động điều hòa và chuyển động tròn đều

Giải chi tiết:

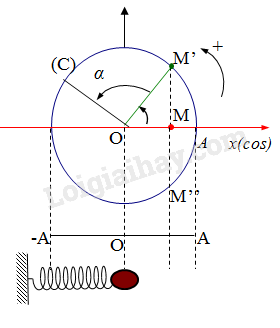
Biên độ dao động điểu hòa của hình chiếu chất điểm lên đường kính bằng bán kính chuyển động

\(A = R = \dfrac{d}{2} = \dfrac{{0,4}}{2} = 0,2(m)\)

Tần số góc  bằng tốc độ góc của chuyển động tròn đều: \(\omega  = \dfrac{v}{R} = \dfrac{{0,6}}{{0,2}} = 3(rad)\)

Chu kì: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{3} = 2,1(s)\)

Chọn D

1.4

Một vật dao động điều hòa theo phương trình \(x=5cos\pi t cm\). Tốc độ của vật có giá trị cực đại là bao nhiêu ?

A. \({-5 \pi cm/s }\)        B. \({5 \pi cm/s }\)        

C. \(5 cm/s\)               D. \(\displaystyle{5 \over \pi }\)cm/s   

Hướng dẫn giải:

Vận dụng công thức tính tốc độ cực đại của chất điểm dao động điều hòa: \({v_{\max }} = A.\omega \)

Giải chi tiết:

Từ phương trình\(x=5cos\pi t cm\) ta có biên độ \(A = 5cm\), tốc độ góc \(\omega  = \pi rad/s\)

Tốc độ cực đại của vật là \(v = A.\omega  = 5\pi (cm/s)\)

Chọn B