Bài 1.1, 1.2, 1.3, 1.4, 1.5 phần bài tập bổ sung trang 115, 116 SBT toán 7 tập 1

Bài I.1

Cho hình bs 10 (hai đường thẳng \(a, b\) song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).

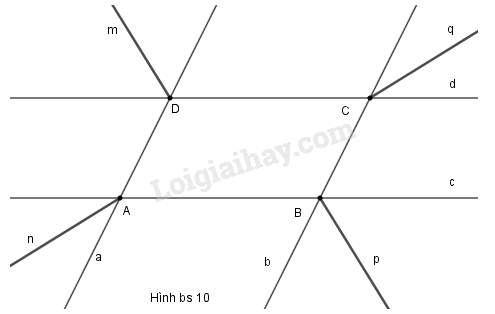
a) Chứng minh: An // Cp và Dm // Bq.

b) Chứng minh: An vuông góc với Bq.  

Phương pháp giải:

Sử dụng dấu hiệu nhận biết hai đường thẳng song song 

Một đường thẳng cắt hai đường thẳng phân biệt tạo thành cặp góc so le trong bằng nhau (cặp góc đồng vị bằng nhau) thì hai đường thẳng đó song song với nhau

Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau

Lời giải chi tiết:

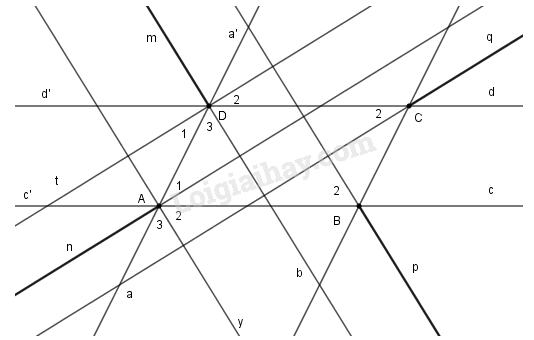
Kẻ thêm các tia đối của tia An, Cq, Bp, Dm và đặt tên như hình vẽ.

Khi đó vì An, Cq, Bp, Dm là các tia phân giác góc A, C, B, D nên ta cũng có các tia đối tương ứng là phân giác của các góc DAB, DCB, ABC, ADC.

Kẻ thêm đường thẳng qua D là phân giác của góc d’DA và đường thẳng qua A là phân giác của góc aAB.

+) Vì \(d//c\)  nên \(\widehat {d'DA} = \widehat {DAB}\) (hai góc so le trong). Mà \(\widehat {{D_1}} = \dfrac{1}{2}\widehat {d'DA},\widehat {{A_1}} = \dfrac{1}{2}\widehat {DAB}\) (tính chất tia phân giác)

Suy ra \(\widehat {{D_1}} = \widehat {{A_1}}\) mà hai góc ở vị trí so le trong nên \(Dt//An\)  (1)

Vì \(a//b\)  nên \(\widehat {a'DC} = \widehat {DCB}\) (hai góc so le trong). Mà \(\widehat {{D_2}} = \dfrac{1}{2}\widehat {a'DC},\widehat {{C_2}} = \dfrac{1}{2}\widehat {DCB}\) (tính chất tia phân giác)

Suy ra \(\widehat {{D_2}} = \widehat {{C_2}}\) mà hai góc ở vị trí so le trong nên \(Dt//Cq\)  (2)

Từ (1) và (2) suy ra \(An//Cq\)

+) Vì \(d//c\)  nên \(\widehat {aAB} = \widehat {ADC}\) (hai góc đồng vị). Mà \(\widehat {{A_3}} = \dfrac{1}{2}\widehat {aAB},\widehat {{D_3}} = \dfrac{1}{2}\widehat {ADC}\) (tính chất tia phân giác)

Suy ra \(\widehat {{D_3}} = \widehat {{A_3}}\) mà hai góc ở vị trí đồng vị nên \(Dm//Ay\)  (3)

Vì \(a//b\)  nên \(\widehat {aAB} = \widehat {ABC}\) (hai góc so le trong). Mà \(\widehat {{A_2}} = \dfrac{1}{2}\widehat {aAB},\widehat {{B_2}} = \dfrac{1}{2}\widehat {ABC}\) (tính chất tia phân giác)

Suy ra \(\widehat {{B_2}} = \widehat {{A_2}}\) mà hai góc ở vị trí so le trong nên \(Bq//Ay\)  (4)

Từ (3) và (4) suy ra \(Dm//Bq\) 

b) Ta có \(\widehat {{D_1}} = \dfrac{1}{2}\widehat {d'Da},\widehat {{D_3}} = \dfrac{1}{2}\widehat {ADC}\)  (tính chất tia phân giác)

Mà \(\widehat {d'DA} + \widehat {ADC} = {180^0}\) (hai góc kề bù)

Nên \(\widehat {{D_1}} + \widehat {{D_3}}\) \( = \dfrac{1}{2}\left( {\widehat {d'DA} + \widehat {ADC}} \right)\) \( = \dfrac{1}{2}{.180^0} = {90^0}\)

Suy ra \(Dt \bot Dm\) mà \(An//Dt\) và \(Dm//Bq\) nên \(An \bot Bq\).

Bài I.2

Trong hình bs 11 ta có tam giác EFG và tia Fm.

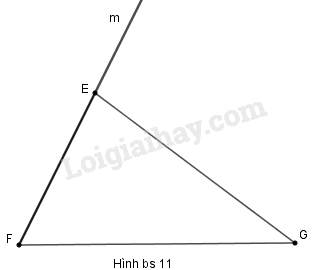
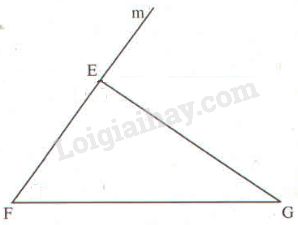
Chứng minh rằng \(\widehat {GEm}=\widehat {EFG} + \widehat {EGF} \)  

Phương pháp giải:

Một đường thẳng cắt hai đường thẳng song song tạo thành cặp góc đồng vị bằng nhau, cặp góc so le trong bằng nhau

Lời giải chi tiết:

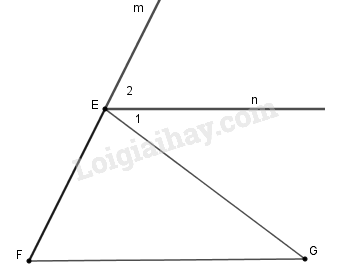
Kẻ tia En//FG

Ta có: \(\widehat {{E_1}} = \widehat G\) (hai góc ở vị trí so le trong)

\(\widehat {{E_2}} = \widehat F\) (hai góc ở vị trí đồng vị)

Suy ra \(\widehat F + \widehat G = \widehat {{E_1}} + \widehat {{E_2}}\)

Hay \(\widehat {EFG} + \widehat {EGF} = \widehat {GEm}\)

Bài I.3

Cho hình bs 12

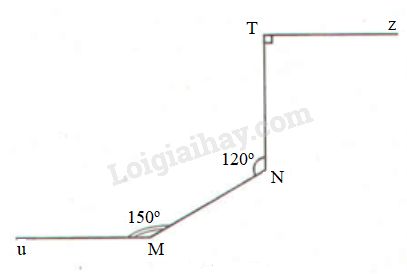
Chứng minh rằng đường thẳng Mu song song với đường thẳng Tz.

Phương pháp giải:

Kẻ tia Nx//Tz

Một đường thẳng cắt hai đường thẳng song song tạo thành cặp góc đồng vị bằng nhau, cặp góc so le trong bằng nhau 

Lời giải chi tiết:

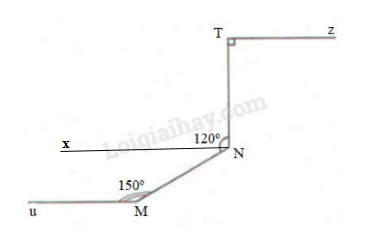
Ta có \(\widehat {xTN} = {90^0}\) mà \(Tz//Nx\) nên \(\widehat {xNT} = \widehat {zTN} = {90^0}\)  (hai góc so le trong) 

Mà tia Nx nằm giữa hai tia NT và NM nên \(\widehat {xNT} + \widehat {MNx} = \widehat {MNT}\)  hay \({90^o} + \widehat {MNx} = {120^0}\) \( \Rightarrow \widehat {MNx} = {120^0} - {90^0} = {30^0}\)

Từ đó \(\widehat {xNM} + \widehat {uMN}\) \( = {30^0} + {150^0} = {180^0}\) mà hai góc ở vị trí trong cùng phía nên \(Mu//Nx\)

Suy ra \(Tz//Mu\) (cùng song song với Nx)

Bài I.4

Mỗi bài từ số I.4 đến số I.10 sau đây đều có bốn lựa chọn là (A), (B), (C) và (D) nhưng chỉ có một trong số đó là đúng. Hãy chọn phương án đúng. 

Hai đường thẳng cắt nhau tạo nên 4 góc (không tính góc bẹt)

(A) đối đỉnh.

(B) đôi một đối đỉnh.

(C) đôi một không kề nhau đối đỉnh.

(D) đôi một chung đỉnh và không chung cạnh đối đỉnh. 

Phương pháp giải:

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của mỗi cạnh góc kia.

Lời giải chi tiết:

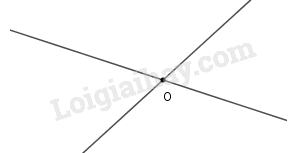
Hai đường thẳng cắt nhau tạo nên 4 góc (không tính góc bẹt) đôi một không kề nhau đối đỉnh. 

Chọn C.

Bài I.5

Hai góc xOy và x’O’y’ có xO // x’O’ và yO // y’O’ (hoặc xO // y’O’ và yO // x’O’) được gọi là hai góc có cạnh tương ứng song song (chẳng hạn hình bs 13). 

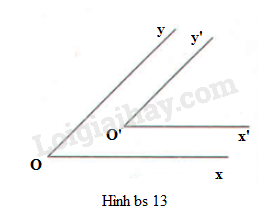
(A) Hai góc nhọn có cạnh tương ứng song song thì bằng nhau.

(B) Hai góc có cạnh tương ứng song song thì bù nhau.

(C) Hai góc có cạnh tương ứng song song thì bằng nhau.

(D) Hai góc có cạnh tương ứng song song thì kề nhau. 

Phương pháp giải:

Quan sát hình vẽ để chọn đáp án đúng.

Lời giải chi tiết:

Hai góc nhọn có cạnh tương ứng song song thì bằng nhau.

Chọn A