Đề số 8 - Đề kiểm tra học kì 1 - Toán 8
Đáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 8
Đề bài
Bài 1 (1,5 điểm)
1.Tính: \(\dfrac{1}{5}{x^2}y\left( {15x{y^2} - 5y + 3xy} \right).\)
2.Phân tích các đa thức sau thành nhân tử:
a)\(5{x^3} - 5x\)
b)\(3{x^2} + 5y - 3xy - 5x\)
Bài 2 (2,0 điểm)Cho \(P = \left( {\dfrac{{x + 2}}{{2x - 4}} + \dfrac{{x - 2}}{{2x{\rm{ + }}4}} + \dfrac{{ - 8}}{{{x^2} - 4}}} \right):\dfrac{4}{{x - 2}}\)
a)Tìm điều kiện của \(x\) để P xác định.
b)Rút gọn biểu thức P.
c)Tính giá trị của biểu thức P khi \(x = - 1\dfrac{1}{3}\)
Bài 3 (2,0 điểm)Cho hai đa thức \(A = 2{x^3} + 5{x^2} - 2x + a\) và \(B = 2{x^2} - x + 1\).
a)Tính giá trị đa thức \(B\) tại \(x = - 1\)
b)Tìm \(a\) để đa thức \(A\) chia hết cho đa thức \(B\).
c)Tìm \(x\)để giá trị đa thức \(B = 1\).
Bài 4 (3,5 điểm)Cho \(\Delta ABC\)có \(\angle A = {90^0}\) và \(AH\) là đường cao. Gọi\(D\) là điểm đối xứng với \(H\) qua \(AB,\,E\) là điểm đối xứng với \(H\) qua \(AC\). Gọi \(I\) là giao điểm của \(AB\) và \(DH,\,K\) là giao điểm của \(AC\) và \(HE\).
a)Tứ giác \(AIHK\) là hình gì? Vì sao?
b)Chứng minh ba điểm \(D,\,A,\,E\) thẳng hàng.
c)Chứng minh: \(CB = B{\rm{D}} + CE\)
d)Biết diện tích tứ giác \(AIHK\) là \(a\)(đvdt). Tính diện tích \(\Delta DHE\) theo \(a\).
Bài 5 (1,0 điểm)
a)Tìm các số\(x,\,y\) thỏa mãn đẳng thức: \(3{x^2} + 3{y^2} + 4xy + 2x - 2y + 2 = 0\)
b)Với \(a,\,b,\,c,\,d\) dương, chứng minh: \(F = \dfrac{a}{{b + c}} + \dfrac{b}{{c + d}} + \dfrac{c}{{d + a}} + \dfrac{d}{{a + b}} \ge 2\)
Lời giải chi tiết
Bài 1.
\(\begin{array}{l}1.\;\;\dfrac{1}{5}{x^2}y\left( {15x{y^2} - 5y + 3xy} \right)\\ = \dfrac{1}{5}{x^2}y.15x{y^2} - \,\,\dfrac{1}{5}{x^2}y.5y + \dfrac{1}{5}{x^2}y.3xy\\\;\; = {x^3}{y^3} - {x^2}{y^2} + \dfrac{3}{5}{x^3}{y^2}.\end{array}\)\(\begin{array}{l}2.\;a)\,\,5{x^3} - 5x = 5x\left( {{x^2} - 1} \right) = 5x\left( {x - 1} \right)\left( {x + 1} \right)\\\;\;b)\,\,3{x^2} + 5y - 3xy - 5x = \left( {3{x^2} - 3xy} \right) - \left( {5x - 5y} \right)\\\;\;\; = 3x\left( {x - y} \right) - 5\left( {x - y} \right) = \left( {3x - 5} \right)\left( {x - y} \right).\\\end{array}\)
Bài 2:
\(\begin{array}{l}a)\;\;P = \left( {\dfrac{{x + 2}}{{2x - 4}} + \dfrac{{x - 2}}{{2x{\rm{ + }}4}} + \dfrac{{ - 8}}{{{x^2} - 4}}} \right):\dfrac{4}{{x - 2}}\\\;\;\;\;\;\;\;\; = \left[ {\dfrac{{x + 2}}{{2\left( {x - 2} \right)}} + \dfrac{{x - 2}}{{2\left( {x + 2} \right)}} - \dfrac{8}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right]:\dfrac{4}{{x - 2}}.\end{array}\)
\(P\)xác định khi và chỉ khi\(\left\{ \begin{array}{l}2x - 4 \ne 0\\2x + 4 \ne 0\\{x^2} - 4 \ne 0\\x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne - 2\\\left( {x - 2} \right)\left( {x + 2} \right) \ne 0\\x \ne 2\end{array} \right. \Leftrightarrow x \ne \pm 2\)
\(\begin{array}{l}b)\;P = \left( {\dfrac{{x + 2}}{{2x - 4}} + \dfrac{{x - 2}}{{2x{\rm{ + }}4}} + \dfrac{{ - 8}}{{{x^2} - 4}}} \right):\dfrac{4}{{x - 2}} \\\;\;\;\;= \dfrac{{{{\left( {x + 2} \right)}^2} + {{\left( {x - 2} \right)}^2} - 16}}{{2\left( {x + 2} \right)\left( {x - 2} \right)}}.\dfrac{{x - 2}}{4}\\\;\;\;\; = \dfrac{{{x^2} + 4x + 4 + {x^2} - 4x + 4 - 16}}{{8\left( {x + 2} \right)}} = \dfrac{{2{x^2} - 8}}{{8\left( {x + 2} \right)}}\\\;\;\;\; = \dfrac{{2\left( {{x^2} - 4} \right)}}{{8\left( {x + 2} \right)}}\\\;\;\;\;\;= \dfrac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{4\left( {x + 2} \right)}} = \dfrac{{x - 2}}{4}.\end{array}\)
c) Thay \(x = - 1\dfrac{1}{3} = - \dfrac{4}{3}\) vào biểu thức \(P\) ta được: \(\dfrac{{\dfrac{{ - 4}}{3} - 2}}{4} = \dfrac{{ - 4 - 6}}{{3.4}} = \dfrac{{ - 10}}{{12}} = - \dfrac{5}{6}.\)
Bài 3
Thay \(x = - 1\)vào \(B = 2{x^2} - x + 1\) ta được: \(B = 2{x^2} - x + 1 = 2.{\left( { - 1} \right)^2} - \left( { - 1} \right) + 1 = 4\)
a) Ta có:
Để \(A\, \vdots \,\left( {2{x^2} - x + 1} \right) \Leftrightarrow a - 3 = 0 \Leftrightarrow a = 3.\)
b) Để \(B = 1 \Leftrightarrow 2\,{x^2} - x + 1 = 1\)
\(\Leftrightarrow 2\,{x^2} - x = 0 \Leftrightarrow x\left( {2\,x - 1} \right) = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{1}{2}\end{array} \right.\)
Bài 4:
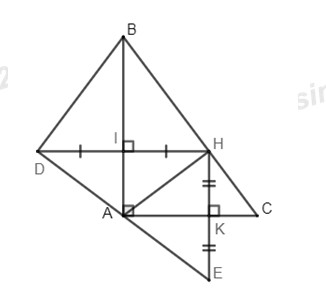
a)Vì \(D\) và \(H\) đối xứng với nhau qua \(AB\left( {gt} \right) \Rightarrow \left\{ \begin{array}{l}DI = IH\\DH \bot AB = \left\{ I \right\}\end{array} \right.\) (tính chất đối xứng trục)
\( \Rightarrow \angle HIA = {90^0}\)
Vì \(H\) và \(E\) đối xứng với nhau qua \(AC\left( {gt} \right) \Rightarrow \left\{ \begin{array}{l}HK = KE\\HE \bot AC = \left\{ K \right\}\end{array} \right.\)(tính chất đối xứng trục)
\( \Rightarrow \angle HKA = {90^0}\)
Xét tứ giác \(AIHK\) có: \(\angle AIH = \angle IAK = \angle AKH = {90^0} \Rightarrow AIHK\) là hình chữ nhật (dhnb)
b)Vì \(D\) và \(H\) đối xứng với nhau qua \(AB\left( {gt} \right) \Rightarrow AB\) là đường trung trực của \(DH\) (tính chất)
\( \Rightarrow DA = AH\) (tính chất)
\( \Rightarrow \Delta A{\rm{D}}H\) cân tại \(A\).
Mà \(AI\) là đường cao nên cũng là tia phân giác của \(\angle DAH\) (tính chất tam giác cân)
\( \Rightarrow \angle DAI = \angle IAH\) (tính chất tia phân giác) (1)
Vì \(E\) và \(H\) đối xứng với nhau qua \(AC\left( {gt} \right) \Rightarrow AC\) là đường trung trực của \(EH\) (tính chất)
\( \Rightarrow HA = AE\) (tính chất điểm thuộc đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta AEH\) cân tại \(A\) (dấu hiệu nhận biết tam giác cân)
Mà \(AK\) là đường cao nên cũng là tia phân giác của \(\angle EAH\) (tính chất tam giác cân)
\( \Rightarrow \angle HAK = \angle KAE\) (tính chất tia phân giác) (2)
Lại có: \(\angle IAH + \angle HAK = {90^0}\left( {gt} \right) \Rightarrow \angle DAI + \angle K{\rm{AE}} = {90^0}\)
\( \Rightarrow \angle DAI + \angle IAH + \angle HAK + \angle K{\rm{AE}} = {180^0} \Rightarrow D,\,A,\,E\)thẳng hàng.
c)Vì \(AB\) là đường trung trực của \(DH\left( {cmt} \right) \Rightarrow DB = BH\) (tính chất)
Vì \(AC\) là đường trung trực của \(EH\left( {cmt} \right) \Rightarrow HC = CE\) (tính chất)
Mà \(BC = BH + HC \Rightarrow BC = B{\rm{D}} + CE\). (đpcm)
d)Do \(\Delta A{\rm{D}}H\) là tam giác cân tại \(A\left( {cmt} \right)\) mà \(AI\) là đường cao nên\( \Rightarrow {S_{\Delta DAI}} = {S_{\Delta HAI}}\)
Lại có, \(\Delta AHE\) cân tại \(A\left( {cmt} \right)\) mà \(AK\) là đường cao nên\( \Rightarrow {S_{\Delta AHK}} = {S_{\Delta AKE}}\)
Do đó ta có: \(\left\{ \begin{array}{l}{S_{AIHK}} = {S_{AIH}} + {S_{AHK}}\\{S_{DEH}} = {S_{AIH}} + {S_{AHK}} + {S_{DAI}} + {S_{AKE}} = 2\left( {{S_{AIH}} + {S_{AHK}}} \right) = 2{S_{AIHK}} = 2a\end{array} \right.\)
Bài 5.
\(\begin{array}{l}a)\,\,3{x^2} + 3{y^2} + 4xy + 2x - 2y + 2 = 0\\ \Leftrightarrow \left( {{x^2} + 2x + 1} \right) + \left( {{y^2} - 2y + 1} \right) + 2\left( {{x^2} + 2xy + {y^2}} \right) = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + 2{\left( {x + y} \right)^2} = 0\end{array}\)
Ta có: \(\left\{ \begin{array}{l}{\left( {x + 1} \right)^2} \ge 0\,\forall \,x\\{\left( {y - 1} \right)^2} \ge 0\,\forall \,y\\{\left( {x + y} \right)^2} \ge 0\,\forall \,x,\,y\end{array} \right. \Rightarrow {\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {x + y} \right)^2} \ge 0\,\forall \,x,\,y\)
Do đó đẳng thức xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x + 1 = 0\\y - 1 = 0\\x + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\\x = - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\)
Vậy \(\left( {x;\;y} \right) = \left( {1;\;1} \right).\)
b) Ta có:
\(\begin{array}{l}F = \dfrac{a}{{b + c}} + \dfrac{b}{{c + d}} + \dfrac{c}{{d + a}} + \dfrac{d}{{a + b}}\\\;\;\; = \left( {\dfrac{a}{{b + c}} + \dfrac{c}{{d + a}}} \right) + \left( {\dfrac{b}{{c + d}} + \dfrac{d}{{a + b}}} \right)\\\;\;\; = \dfrac{{a\left( {d + a} \right) + c\left( {b + c} \right)}}{{\left( {b + c} \right)\left( {d + a} \right)}} + \dfrac{{b\left( {a + b} \right) + d\left( {c + d} \right)}}{{\left( {c + d} \right)\left( {a + b} \right)}}\\\;\;\; = \dfrac{{{a^2} + {c^2} + ad + bc}}{{\left( {b + c} \right)\left( {d + a} \right)}} + \dfrac{{{b^2} + {d^2} + ab + cd}}{{\left( {c + d} \right)\left( {a + b} \right)}}.\end{array}\)
Áp dụng bất đẳng thức Cô-si cho hai số \(x\) và \(y\) dương ta có:\({\left( {x + y} \right)^2} \ge 4xy.\)
Áp dụng bất đẳng thức trên cho hai số \(\left( {b + c} \right)\) và \(\left( {d + a} \right)\) ta có:
\(\begin{array}{l}\;\;\;\;{\left[ {\left( {b + c} \right) + \left( {a + d} \right)} \right]^2} \ge 4\left( {b + c} \right)\left( {a + d} \right)\\ \Leftrightarrow \left( {b + a} \right)\left( {a + d} \right) \le \dfrac{{{{\left( {a + b + c + d} \right)}^2}}}{4}.\end{array}\)
Tương tự ta có: \(\left( {c + d} \right)\left( {a + b} \right) \le \dfrac{{{{\left( {a + b + c + d} \right)}^2}}}{4}.\)
\(\begin{array}{l} \Rightarrow F \ge \dfrac{{{a^2} + {c^2} + ad + bc}}{{\dfrac{1}{4}\left( {b + c + d + a} \right)}} + \dfrac{{{b^2} + {d^2} + ab + cd}}{{\dfrac{1}{4}{{\left( {c + d + a + b} \right)}^2}}}\\\;\;\;\;\;\;\;\; = \dfrac{{4\left( {{a^2} + {b^2} + {c^2} + {d^2} + ab + bc + cd + ad} \right)}}{{{{\left( {a + b + c + d} \right)}^2}}}\\\;\;\;\;\;\;\;\; = \dfrac{{2\left( {{a^2} + {b^2} + {c^2} + {d^2} + 2ab + 2bc + 2cd + 2da + 2bd + 2ac} \right) + 2\left( {{a^2} + {b^2} + {c^2} + {d^2} - 2bd - 2ca} \right)}}{{{{\left( {a + b + c + d} \right)}^2}}}\\\;\;\;\;\;\;\;\; = \dfrac{{2{{\left( {a + b + c + d} \right)}^2} + 2\left[ {{{\left( {a - c} \right)}^2} + {{\left( {b - d} \right)}^2}} \right]}}{{{{\left( {a + b + c + d} \right)}^2}}}\\\;\;\;\;\;\;\;\; = 2 + \dfrac{{2\left[ {{{\left( {a - c} \right)}^2} + {{\left( {b - d} \right)}^2}} \right]}}{{{{\left( {a + b + c + d} \right)}^2}}}.\end{array}\)
Ta có: \({\left( {a - c} \right)^2} + {\left( {b - d} \right)^2} \ge 0\)
\( \Rightarrow F \ge 2.\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a - c = 0\\b - d = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = c\\b = d\end{array} \right..\)
Vậy \(F \ge 2\;\;\left( {dpcm} \right).\)
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại TimDapAn.com
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề số 8 - Đề kiểm tra học kì 1 - Toán 8 timdapan.com"







