Đề số 2 - Đề kiểm tra học kì 1 - Toán 8

Đề bài

Bài 3 (1,5 điểm)

a) Thực hiện phép chia đa thức \(A = {x^3} - 7x + 3 - {x^2}\) cho đa thức \(B = x - 3\) .

b) Gọi Q là thương của phép chia A cho B. Chứng minh \(Q + 3\) luôn nhận giá trị dương với mọi \(x \ne 3.\)

Bài 4 (3 điểm)Cho \(\Delta ABC\)vuông tại A \(\left( {AB < AC} \right)\). Gọi \(M,\,N,K\) thứ tự là trung điểm của \(AB,\,AC\)  và \(BC\).

a)Chứng minh \(KN = \dfrac{1}{2}AB\)và \(ABKN\) là hình thang vuông.

b)Qua \(M\) kẻ đường thẳng song song với \(BN\), cắt tia \(KN\) tại \(Q\). Chứng minh \(AKCQ\) là hình thoi.

c)\(MN\) cắt \(BQ\) tại \(O\) , \(AK\) cắt \(BN\) tại \(I\). Biết \(BC = 24\,cm\). Tính độ dài \(OI\).

Bài 5 (1 điểm)Trong hình vẽ sau, hai địa điểm A và B cách nhau \(100\,km\). Một xe ô tô khởi hành từ B đến A với vận tốc \(40\,km/h\). Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường vuông góc với AB với vận tốc \(20\,km/h\). Gọi C, D thứ tự là vị trí của xe ô tô và xe đạp điện vào thời điểm t(h) sau khi khởi hành. Giả sử vận tốc của hai xe không thay đổi trong quá trình di chuyển.

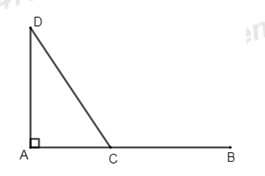
a)Viết biểu thức đại số biểu diễn độ dài \(AC,\,A{\rm{D}}\)  theo \(t\).

b)Hỏi sau bao lâu (tính từ lúc khởi hành) khoảng cách \(C{\rm{D}}\) là ngắn nhất? Giải thích.

Lời giải chi tiết

Bài 1.

a) \(3{a^3}{b^2} - 15{a^2}{b^3} = 3{a^2}{b^2}\left( {a - 5b} \right)\)

b) \(5{x^2} - 10x + 5 - 20{y^2}\)

\(= 5\left( {{x^2} - 2x + 1 - 4{y^2}} \right)\)

\(= 5\left[ {{{\left( {x - 1} \right)}^2} - {{\left( {2y} \right)}^2}} \right] \)

\(= 5\left( {x - 1 - 2y} \right)\left( {x - 1 + 2y} \right)\)

Bài 2.

\(\begin{array}{l}a)\,\,\left( {x - 3} \right)\left( {x - 6} \right) + x\left( {4 - x} \right)\\ = {x^2} - 6x - 3x + 18 + 4x - {x^2}\\ =  - 5x + 18.\end{array}\)\(\begin{array}{l}c)\,\,{\left( {x + 4} \right)^2} - 25 + \left( {3 + x} \right)\left( {3 - x} \right)\\ = {x^2} + 8x + 16 - 25 + 9 - {x^2}\\ = 8x.\end{array}\)

\(\begin{array}{l}b)\,\,\dfrac{{5x}}{{x - 1}} + \dfrac{{3x - 8}}{{x - 1}}\;\;\;\left( {DK:\;\;x \ne 1} \right)\\ = \dfrac{{5x + 3x - 8}}{{x - 1}}\\ = \dfrac{{8x - 8}}{{x - 1}}\\ = \dfrac{{8\left( {x - 1} \right)}}{{x - 1}} = 8.\end{array}\)\(\begin{array}{l}d)\,\,\dfrac{{2x - 1}}{x} + \dfrac{{2x + 5}}{{4x - 3}} + \dfrac{{2{x^2} + x + 3}}{{3x - 4{x^2}}}\;\;\;\;\left( {Dk:\;\;x \ne 0,\;\;x \ne \dfrac{3}{4}} \right)\\ = \dfrac{{\left( {2x - 1} \right)\left( {3 - 4x} \right) - x\left( {2x + 5} \right) + \left( {2{x^2} + x + 3} \right)}}{{x\left( {3 - 4x} \right)}}\\ = \dfrac{{6x - 8{x^2} - 3 + 4x - 2{x^2} - 5x + 2{x^2} + x + 3}}{{x\left( {3 - 4x} \right)}}\\ = \dfrac{{ - 8{{\rm{x}}^2} + 6{\rm{x}}}}{{{\rm{x}}\left( {3 - 4{\rm{x}}} \right)}}\\ = \dfrac{{{\rm{2}}x\left( { - 4x + 3} \right)}}{{x\left( {3 - 4x} \right)}} = 2\end{array}\)

Bài 3.

a)Thực hiện phép chia đa thức \(A = {x^3} - 7x + 3 - {x^2}\) cho đa thức \(B = x - 3\) .

b)Ta có:

\(Q = {x^2} + 2{\rm{x}} - 1 \Rightarrow Q + 3 = {x^2} + 2x - 1 + 3 = {x^2} + 2x + 2\)

\( \Rightarrow Q = {x^2} + 2x + 1 + 1 = {\left( {x + 1} \right)^2} + 1.\)

Vì \({\left( {x + 1} \right)^2} \ge 0\,\forall x \Rightarrow {\left( {x + 1} \right)^2} + 1 > 0\,\forall x \ne 3 \Rightarrow Q + 3 > 0\,\forall x \ne 3.\)

Bài 4.

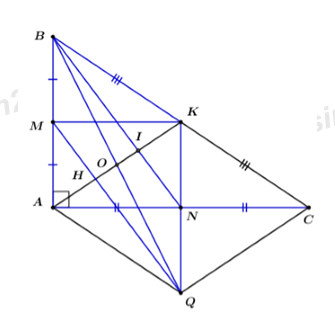
a) Vì \(N,\,K\) lần lượt là trung điểm của \(AC\)  và \(BC\) (gt)

\( \Rightarrow NK\)là đường trung bình của \(\Delta ACB\) (dấu hiệu nhận biết đường trung bình của tam giác)

\( \Rightarrow \left\{ \begin{array}{l}NK = \dfrac{{AB}}{2}\left( * \right)\\NK//AB\end{array} \right.\) (tính chất đường trung bình của tam giác)

Ta có: \(NK//AB\left( {cmt} \right) \Rightarrow \)tứ giác \(NKBA\) là hình thang (dấu hiệu nhận biết hình thang)

Lại có: \(\angle NAB = {90^0}\left( {gt} \right) \Rightarrow \) hình thang \(NKBA\) là hình thang vuông (dấu hiệu nhận biết hình thang vuông)

b)Ta có: \(AB//NK\left( {cmt} \right) \Rightarrow QN//MB\) mà \(QM//NB\left( {gt} \right) \Rightarrow \) tứ giác \(MBNQ\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

\( \Rightarrow QN = MB = \dfrac{{AB}}{2}\left( {**} \right)\) (tính chất hình bình hành)

Từ \(\left( * \right)\) và \(\left( {**} \right) \Rightarrow QN = NK\), lại có \(AN = NC\left( {gt} \right) \Rightarrow AQCK\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Mặt khác, xét \({\Delta _v}ABC\) có \(AK\) là trung tuyến (gt) suy ra \(AK = \dfrac{{BC}}{2}\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)

Mà \(KC = \dfrac{{BC}}{2}\left( {gt} \right) \Rightarrow AK = CK\)

\( \Rightarrow \) hình bình hành \(AQCK\) là hình thoi (dấu hiệu nhận biết hình thoi)

c)Gọi \(H\) là giao điểm của \(MQ\)  và \(AK\)

Vì \(BNQM\) là hình bình hành (cmt)

\( \Rightarrow \left\{ \begin{array}{l}BN//MQ\\BO = OQ\end{array} \right.\) (tính chất hình bình hành) \( \Rightarrow \angle IBO = \angle OQH\) (so le trong)

Xét \(\Delta OIB\) và \(\Delta OHQ\)có:

\(\angle IBO = \angle OQH\) (cmt)

\(BO = OQ\left( {cmt} \right)\)

\(\angle BOI = \angle HOQ\) (đối đỉnh)

\( \Rightarrow \Delta OIB = \Delta OHQ\left( {g - c - g} \right) \)

\(\Rightarrow OI = OH\) (2 cạnh tương ứng)

Xét \(\Delta IAB\) có:

\(MH//IB\) (do \(MQ//BN\))

\(M\) là trung điểm của \(AB\left( {gt} \right)\)

\( \Rightarrow \)\(H\)  là trung điểm của \(AI\)(trong tam giác, đường thẳng đi qua trung điểm của cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)

\( \Rightarrow AH = HI\left( 1 \right)\) (tính chất trung điểm của đoạn thẳng)

Vì \(AKCQ\) là hình thoi (cmt) mà \(N\) là trung điểm của \(AC\left( {gt} \right)\) và \(AC \cap KQ = \left\{ N \right\} \Rightarrow N\) là trung điểm của \(AC\) (tính chất hình thoi)

Xét \(\Delta KCQ\) có:

\(IN//HQ\) (do \(MQ//BN\))

\(N\) là trung điểm của \(KQ\left( {cmt} \right)\)

\( \Rightarrow I\) là trung điểm của \(HK\) (trong tam giác, đường thẳng đi qua trung điểm của cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)

\( \Rightarrow KI = HI\left( 2 \right)\) (tính chất trung điểm của đoạn thẳng)

Từ \(\left( 1 \right)\) và \(\left( 2 \right) \Rightarrow AH = HI = IK = \dfrac{1}{3}AK\)\(\)

Xét \({\Delta _v}ABC\) có: \(AK = \dfrac{{BC}}{2} = 12cm\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)

\( \Rightarrow AH = HI = IK = \dfrac{1}{3}AK = \dfrac{{12}}{3} = 4cm\)

Ta có: \(NK//AB\left( {cmt} \right) \Rightarrow KQ//AB\left( 3 \right)\)

Do \(AKCQ\) là hình thoi (cmt) và \(N\) là giao điểm của hai đường chéo \(AC\) và \(KQ \Rightarrow KN = \dfrac{1}{2}KQ\) (tính chất hình thoi)

Mà \(KN = \dfrac{1}{2}AB\left( {cmt} \right) \) \(\Rightarrow KQ = AB\left( 4 \right)\)

Từ \(\left( 3 \right)\) và \(\left( 4 \right) \Rightarrow ABKQ\)là hình bình hành (dấu hiệu nhận biết hình bình hành)

\( \Rightarrow O\) là trung điểm của \(AK\) (tính chất hình bình hành)

\( \Rightarrow AO = OK\) (tính chất trung điểm)

Lại có \(\left\{ \begin{array}{l}OI = OK - KI\\OH = OA - AH\end{array} \right.\)

Mà \(AH = IK\;\left( {cmt} \right) \Rightarrow OI = OH = \dfrac{{IH}}{2} = \dfrac{4}{2} = 2\;cm.\)

Bài 5.

a)Quãng đường BC mà ô tô đi được trong thời gian t giờ là: 40t (km)

Vậy độ dài của quãng đường AC là: \(100 - 40t\left( {km} \right)\)

Quãng đường AD mà xe đạp điện đi được trong thời gian t giờ là: \(20t\left( {km} \right)\)

b)Áp dụng định lí Py-ta-go cho tam giác ADC vuông tại A ta có:

\(\begin{array}{l}DC = \sqrt {{{\left( {100 - 40t} \right)}^2} + 400{t^2}}  \\\;\;\;\;\;= \sqrt {10000 - 8000t + 1600{t^2} + 400{t^2}} \\\;\;\;\;\; = \sqrt {2000{t^2} - 8000t + 10000}  \\\;\;\;\;= 20\sqrt 5 \sqrt {{t^2} - 4t + 5} .\end{array}\)

Để độ dài đoạn DC ngắn nhất thì \(\sqrt {{t^2} - 4t + 5} \) đạt giá trị nhỏ nhất. Ta có :

\(\sqrt {{t^2} - 4t + 5}  = \sqrt {{{\left( {t - 2} \right)}^2} + 1}  \ge 1\,\forall t\) nên DC đạt giá trị nhỏ nhất \( \Leftrightarrow t - 2 = 0 \Leftrightarrow t = 2.\)

Vậy sau khi 2 xe khởi hành được 2 giờ thì khoảng cách CD ngắn nhất.

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại TimDapAn.com