Đề số 19 - Đề kiểm tra học kì 1 - Toán 8
Đáp án và lời giải chi tiết Đề số 19 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 8
Đề bài
Bài 1. Phân tích đa thức \({a^3} + 3{a^2} + 3a + 1\) thành nhân tử.
Bài 2. Rút gọn và tính giá trị của biểu thức \(A = {{2x} \over {1 - {x^3}}} + {1 \over {{x^2} - x}} - {1 \over {{x^2} + x + 1}}\) khi x = 10.
Bài 3. Cho biểu thức \(P = {2 \over {{x^4} - 1}} + {1 \over {1 - {x^2}}}.\)
a) Tìm điều kiện xác định của biểu thức P.
b) Chứng minh giá trị của P luôn âm với \(x \ne \pm 1.\)
Bài 4. Chứng minh rằng biểu thức \(Q = \left( {{x^2} - 1} \right)\left( {{1 \over {x - 1}} - {1 \over {x + 1}} + 1} \right)\) luôn dương với \(x \ne \pm 1.\)
Bài 5. Cho tứ giác ABCD. Hai đường chéo AC và BD vuông góc với nhau . Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA.
a) Tứ giác MNPQ là hình gì? Vì sao ?
b) Để MNPQ là hình vuông thì tứ giác ABCD cần có điều kiện gì ?
Bài 6. Cho hình bình hành ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của cạnh AB và CD.
a) Chứng tỏ tứ giác AECF là hình bình hành.
b) Chứng tỏ AF vuông góc với DE.
c) Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE, chứng tỏ EF = MN.
d) Tính tỉ số diện tích của \(\Delta BEF\) và diện tích hình bình hành ABCD.
Lời giải chi tiết
Bài 1. \({a^3} + 3{a^2} + 3a + 1 = {\left( {a + 1} \right)^3}\)
Bài 2. Điều kiện : \(x \ne 0;x \ne 1.\)
\(A = {{2{x^2} - \left( {{x^2} + x + 1} \right) - x\left( {x - 1} \right)} \over {x\left( {1 - {x^3}} \right)}} = {{ - 1} \over {x\left( {1 - {x^3}} \right)}} = {1 \over {x\left( {{x^3} - 1} \right)}}\)
Khi \(x = 10 \Rightarrow A = {1 \over {9990}}.\)
Bài 3.
a) Ta có : \({x^4} - 1 = \left( {{x^2} + 1} \right)\left( {{x^2} - 1} \right),\)trong đó : \({x^2} + 1 > 0,\) với mọi x.
Vậy điều kiện : \({x^4} - 1 \ne 0\) và \(1 - {x^2} \ne 0\) là \({x^2} - 1 \ne 0\)
\({x^2} - 1 = \left( {x - 1} \right)\left( {x + 1} \right) \ne 0 \Rightarrow x - 1 \ne 0\) và \(x + 1 \ne 0 \Rightarrow x \ne \pm 1\) .
b) \(P = {2 \over {\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right)}} - {1 \over {{x^2} - 1}} = {{2 - \left( {{x^2} + 1} \right)} \over {\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right)}} = {{2 - {x^2} - 1} \over {\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right)}}\)
\( = {{ - \left( {{x^2} - 1} \right)} \over {\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right)}} = {{ - 1} \over {{x^2} + 1}}.\)
Vì \({x^2} + 1 > 0\) nên P < 0, với mọi \(x \ne \pm 1.\)
Bài 4. Ta có : \(Q = {{{x^2} - 1} \over {x - 1}} - {{{x^2} - 1} \over {x + 1}} + {x^2} - 1 \)\(\,= {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {x - 1}} - {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {x + 1}} + {x^2} - 1\)
\( = x + 1 - x + 1 + {x^2} - 1 = {x^2} + 1 > 0,\) với mọi \(x \ne \pm 1\) .
Bài 5.
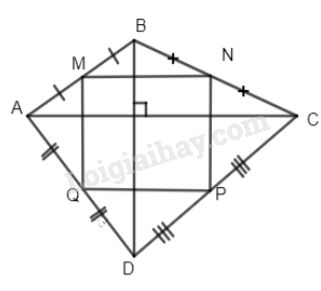
a) Ta có MN là đường trung bình của \(\Delta ABC\)
\( \Rightarrow MN\parallel AC\) và \(MN = {1 \over 2}AC\)
Tương tự \(QP\parallel AC\) và \(QP = {1 \over 2}AC\)
Do đó MNPQ là hình bình hành.
Chứng minh tương tự ta có MQ là đường trung bình của \(\Delta ADB\) nên \(MQ\parallel BD\) mà \(BD \bot AC\left( {gt} \right) \Rightarrow MQ \bot MN.\)
Vậy tứ giác MNPQ là hình chữ nhật.
b) Hình chữ nhật MNPQ là hình vuông \( \Leftrightarrow MN = MQ \Leftrightarrow AC = BD\)
\( \Leftrightarrow ABCD\) là tứ giác có hai đường chéo vuông góc.
Bài 6.

a) Ta có E, F lần lượt là trung điểm của AB và DC mà AB = CD và \(AB\parallel CD\)
\( \Rightarrow AE = CF\) và \(AE\parallel CF\).
Do đó AECF là hình bình hành.
b) Tương tự như chứng minh trên ta có \(AE\parallel DF\) và AE = DF nên AEFD là hình bình hành.
Lại có AB = 2AD (gt) mà E là trung điểm AB nên AE = AD.
Do đó AEFD là hình thoi \( \Leftrightarrow AF \bot DE.\)
c) Ta có \(AF\parallel CE\left( {cmt} \right),\) tương tự ta có EBFD là hình bình hành
\( \Rightarrow ED\parallel BF.\)
Do đó tứ giác ENFM là hình bình hành, lại có \(\widehat {EMF} = {90^ \circ }\left( {cmt} \right)\)
Vậy tứ giác ENFM là hình chữ nhật \( \Rightarrow {\rm{EF = MN}}{\rm{.}}\)
d)Ta có các tam giác sau đây bằng nhau:
\(\Delta BEF = \Delta FCB = \Delta AEF = \Delta FDA\)
\( \Rightarrow {S_{BEF}} = {S_{FCB}} = {S_{AEF}} = {S_{FDA}} = {1 \over 4}{S_{ABCD}}\)
Do đó \({{{S_{BEF}}} \over {{S_{ABCD}}}} = {1 \over 4}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề số 19 - Đề kiểm tra học kì 1 - Toán 8 timdapan.com"







