Đề số 4 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10
Đáp án và lời giải chi tiết Đề số 4 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10
Đề bài
I. TRẮC NGHIỆM (4,0 điểm) Chọn đáp án đúng trong mỗi câu sau:
Câu 1 (TH): Cho hai số a,b thỏa mãn \(\frac{{{a^2} + {b^2}}}{2} \le {\left( {\frac{{a + b}}{2}} \right)^2}\). Chọn mệnh đề đúng trong các mệnh đề sau:
A. \(a < b\)
B. \(a > b\)
C. \(a = b\)
D. \(a \ne b\)
Câu 2 (VD): Cho hàm số \(f\left( x \right) = \frac{{x + 2019}}{{x - 2019}}\). Chọn khẳng định đúng trong các khẳng định sau :
A. \(f\left( x \right) > 0 \Leftrightarrow x > 2019\)
B. \(f\left( x \right) > 0 \Leftrightarrow f\left( x \right) > - 2019\)
C. \(f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x < - 2019\\x > 2019\end{array} \right.\)
D. \(f\left( x \right) < 0 \Leftrightarrow - 2019 < x < 2019\)
Câu 3 (NB): Điều kiện xác định của bất phương trình \(2018\sqrt {x + 2} > 2019{x^2} + \frac{1}{{x - 2}}\) là:
A. \(x \ge - 2\)
B. \(x > 2\)
C. \(x \ge - 2\) và \(x \ne 2\)
D. \(x \ge 2\)
Câu 4 (VD): Xác định tất cả các giá trị của tham số m để phương trình \(\left( {m + 1} \right){x^2} - 2\left( {m + 2} \right) + m + 4 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) và \({x_1} + {x_2} + {x_1}{x_2} < 2\).
A. \(m < - 6\)
B. \( - 6 < m < - 1\)
C. \( - \frac{8}{3} < m < - 1\)
D. Không tồn tại m
Câu 5 (TH): Có bao nhiêu giá trị của tham số m để hệ bất phương trình \(\left\{ \begin{array}{l}x - 3 \ge m\\\left( {m - 2} \right)x \le 3m - 3\end{array} \right.\) có nghiệm duy nhất ?
A. \(2\)
B. \(1\)
C. \(0\)
D. Đáp án khác
Câu 6 (TH): Kết quả điểm kiểm tra môn Toán trong một kỳ thi của 200 em học sinh được trình bày ở bảng sau:
Số trung vị của bảng phân bố tần suất nói trên là:
A. \(8\) B. \(7\) C. \(6\) D. Đáp án khác
Câu 7 (NB): Chọn công thức sai trong các công thức sau:
A. \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\)
B. \(\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)
C. \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\)
D. \(\cos a - \cos b = 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)
Câu 8 (VD): Rút gọn biểu thức \(M = \cos \left( {x + \frac{\pi }{4}} \right) + \sin \left( {x - \frac{\pi }{4}} \right)\)
A. \(M = \cos x + \sin x\)
B. \(M = \sqrt 2 \cos x\)
C. \(M = 0\)
D. \(M = \sqrt 2 \cos x + \sqrt 2 \sin x\)
Câu 9 (VD): Cho \(\sin a = \frac{4}{5},\,\,\cos b = \frac{8}{{17}}\) với \(\frac{\pi }{2} < a < \pi \) và \(0 < b < \frac{\pi }{2}\). Giá trị của \(\sin \left( {a + b} \right)\) bằng:
A. \( - \frac{{13}}{{85}}\)
B. \(\frac{{77}}{{85}}\)
C. \( - \frac{{77}}{{85}}\)
D. \(\frac{{13}}{{85}}\)
Câu 10 (TH): Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng \(d:x + 5y - 2019 = 0\). Tìm mệnh đề sai trong các mệnh đề sau:
A. \(\overrightarrow n = \left( {1;5} \right)\) là một vectơ pháp tuyến của d
B. \(\overrightarrow u = \left( { - 5;1} \right)\) là một vectơ chỉ phương của d
C. d có hệ số góc \(k = 5\)
D. d song song với đường thẳng \(\Delta :x + 5y = 0\)
Câu 11 (NB): Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm \(A\left( {0;2} \right),\,\,B\left( { - 3;0} \right)\). Phương trình đường thẳng AB là:
A. \(\frac{x}{2} + \frac{y}{{ - 3}} = 1\)
B. \(\frac{x}{{ - 3}} + \frac{y}{2} = 1\)
C. \(\frac{x}{3} + \frac{y}{{ - 2}} = 1\)
D. \(\frac{x}{{ - 2}} + \frac{y}{3} = 1\)
Câu 12 (VD): Trong mặt phẳng với hệ tọa độ Oxy, cho ba đường thẳng lần lượt có phương trình \({d_1}:5x - 6y - 4 = 0\), \({d_2}:x + 2y - 4 = 0\) và \({d_3}:mx - \left( {2m - 1} \right)y + 9m - 19 = 0\) (m là tham số). Tìm tất cả các giá trị của tham số m để ba đường thẳng đã cho cùng đi qua một điểm.
A. \(m = 1\).
B. \(m = - 1\).
C. \(m = - 2\).
D. \(m = 2\).
Câu 13 (VD): Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm \(A\left( {1;1} \right),\,\,B\left( { - 2;4} \right)\) và đường thẳng \(\Delta :mx - y + 3 = 0\). Tìm tất cả các giá trị của tham số m để \(\Delta \) cách đều 2 điểm A, B.
A. \(\left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\)
B. \(\left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\)
C. \(\left[ \begin{array}{l}m = - 1\\m = 1\end{array} \right.\)
D. \(\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\)
Câu 14 (VD): Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng \(\Delta :3x + 4y - 5 = 0\) và điểm \(I\left( {2;1} \right)\). Đường tròn \(\left( C \right)\) có tâm \(I\) và tiếp xúc với đường thẳng \(\Delta \) có phương trình là:
A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\)
B. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{1}{{25}}\)
C. \({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 1\)
D. \({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = \frac{1}{{25}}\)
Câu 15 (VD): Cho Elip \(\left( E \right)\) có độ dài trục lớn bằng 12, độ dài trục bé bằng tiêu cự. Phương trình chính tắc của \(\left( E \right)\) là:
A. \(\frac{{{x^2}}}{{144}} + \frac{{{y^2}}}{{72}} = 1\)
B. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{18}} = 1\)
C. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{36}} = 1\)
D. \(\frac{{{x^2}}}{{144}} + \frac{{{y^2}}}{{144}} = 1\)
Câu 16 (VD): Cho đường tròn \(\left( C \right)\) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 1\). Điều kiện của m để qua điểm \(A\left( {m;1 - m} \right)\) kẻ được 2 tiếp tuyến với \(\left( C \right)\) tạo với nhau một góc \({90^o}\) là:
A. \(\left[ \begin{array}{l}m = 1\\m = 3\end{array} \right.\)
B. \(m = 0\)
C. \(\left[ \begin{array}{l}m = - 1\\m = - 3\end{array} \right.\)
D. Không có giá trị phù hợp
II. PHẦN TỰ LUẬN (6,0 điểm – 6,0 điểm)
Bài 1 (VD). (1,5 điểm – 1,5 điểm)
a) Giải hệ bất phương trình sau trên tập số thực : \(\left\{ \begin{array}{l}\left( {x - 3} \right)\left( {{x^2} - 4x + 4} \right)\left( {{x^2} + x - 2} \right) > 0\\\left| {x - 1} \right| < x + 1\end{array} \right.\)
b) Giải bất phương trình sau trên tập số thực : \(\sqrt { - 3{x^2} + 7x - 2} + x < 2\)
Bài 2 (VD). (1,5 điểm – 2,0 điểm)
a) Chứng minh đẳng thức: \(\frac{{2{{\sin }^2}\left( {x + \frac{\pi }{4}} \right) - 1}}{{\cot x - \sin x.\cos x}} = 2{\tan ^2}x\) khi các biểu thức đều xác định.
b) Tìm các giá trị của tham số m để bất phương trình \( - 1 \le \frac{{{x^2} - 2x - m}}{{{x^2} + 2x + 2019}} < 2\) nghiệm đúng với mọi số thực x.
Bài 3 (VD). (2,5 điểm – 2,5 điểm)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng \(d:2x - y - 5 = 0\) và hai điểm \(A\left( {1;2} \right),\,\,B\left( {4;1} \right)\)
a) (1 điểm) Viết phương trình đường trung trực đoạn thẳng AB.
b) (1 điểm) Viết phương trình đường tròn \(\left( C \right)\) có tâm thuộc đường thẳng d và đi qua 2 điểm A, B.
c) (0,5 điểm) Viết phương trình tiếp tuyến của \(\left( C \right)\) biết tiếp tuyến vuông góc với đường thẳng \(d':x + y + 2019 = 0\)
Bài 4 (VDC). (0,5 điểm – 0 điểm)(Chỉ dành cho các lớp 10 Tin, L1, L2, H1, H2)
Tính các góc của \(\Delta ABC\) biết
\(\left( {1 + \frac{1}{{\sin A}}} \right)\left( {1 + \frac{1}{{\sin B}}} \right)\left( {1 + \frac{1}{{\sin C}}} \right) \)\(= {\left( {1 + \frac{1}{{\sqrt[3]{{\sin A\sin B\sin C}}}}} \right)^3}\).
Lời giải chi tiết
I. PHẦN TRẮC NGHIỆM
|
1. C |
2. D |
3. C |
4. B |
|
5. B |
6. D |
7. D |
8. C |
|
9. A |
10. C |
11. B |
12. D |
|
13. C |
14. A |
15. B |
16. A |
Câu 1:
Phương pháp:
Sử dụng phương pháp biến đổi tương đương để biến đổi bất đẳng thức.
Cách giải:
\(\begin{array}{l}\frac{{{a^2} + {b^2}}}{2} \le {\left( {\frac{{a + b}}{2}} \right)^2}\\ \Leftrightarrow \frac{{{a^2} + {b^2}}}{2} \le \frac{{{a^2} + {b^2} + 2ab}}{4}\\ \Leftrightarrow \frac{{2{a^2} + 2{b^2}}}{4} - \frac{{{a^2} + {b^2} + 2ab}}{4} \le 0\\ \Leftrightarrow \frac{{{a^2} + {b^2} - 2ab}}{4} \le 0\\ \Leftrightarrow {\left( {a - b} \right)^2} \le 0 \Leftrightarrow a - b = 0 \Leftrightarrow a = b\end{array}\)
Chọn C.
Câu 2:
Phương pháp:
Giải BPT \(f\left( x \right) > 0\) để tìm tập nghiệm của bất phương trình.
Cách giải:
\(f\left( x \right) = \frac{{x + 2019}}{{x - 2019}} < 0\)\( \Leftrightarrow - 2019 < x < 2019\)
Chọn D.
Câu 3:
Phương pháp:
\(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\)
\(\frac{1}{{g\left( x \right)}}\) xác định \( \Leftrightarrow g\left( x \right) \ne 0\)
Cách giải:
\(2018\sqrt {x + 2} > 2019{x^2} + \frac{1}{{x - 2}}\)
ĐKXĐ: \(\left\{ \begin{array}{l}x + 2 \ge 0\\x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne 2\end{array} \right.\)
Chọn C.
Câu 4:
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0\)
Sử dụng hệ thức Vi-ét biến đổi và thế vào biểu thức bài cho để giải phương trình tìm m.
Cách giải:
Để phương trình \(\left( {m + 1} \right){x^2} - 2\left( {m + 2} \right) + m + 4 = 0\) có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 0\\\Delta ' = {\left( {m + 2} \right)^2} - \left( {m + 1} \right)\left( {m + 4} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\{m^2} + 4m + 4 - {m^2} - 5m - 4 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\ - m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\m < 0\end{array} \right.\,\end{array}\)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{2m + 4}}{{m + 1}}\\{x_1}{x_2} = \frac{{m + 4}}{{m + 1}}\end{array} \right.\)
Ta có: \({x_1} + {x_2} + {x_1}{x_2} < 2\)
\(\begin{array}{l} \Leftrightarrow \frac{{2m + 4}}{{m + 1}} + \frac{{m + 4}}{{m + 1}} < 2\\ \Leftrightarrow \frac{{m + 6}}{{m + 1}} < 0 \Leftrightarrow - 6 < m < - 1\end{array}\)
Kết hợp các điều kiện ta được \( - 6 < m < - 1\) thỏa mãn bài toán.
Chọn B.
Câu 5:
Phương pháp:
Biến đổi hệ BPT và biện luận.
Cách giải:
+) Với \(m = 2\) HPT trở thành : \(\left\{ \begin{array}{l}x - 3 \ge 2\\0 \le 3\end{array} \right. \Leftrightarrow x \ge 5\) không có nghiệm duy nhất.
+) Với \(m > 2\) ta có : \(\left\{ \begin{array}{l}x - 3 \ge m\\\left( {m - 2} \right)x \le 3m - 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge m + 3\\x \le \frac{{3m - 3}}{{m - 2}}\end{array} \right.\)
HPT có nghiệm duy nhất \( \Leftrightarrow m + 3 = \frac{{3m - 3}}{{m - 2}}\)
\(\begin{array}{l} \Leftrightarrow {m^2} + m - 6 = 3m - 3\\ \Leftrightarrow {m^2} - 2m - 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\left( {tm} \right)\\m = - 1\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
+) Với \(m < 2\) ta có : \(\left\{ \begin{array}{l}x - 3 \ge m\\\left( {m - 2} \right)x \le 3m - 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge m + 3\\x \ge \frac{{3m - 3}}{{m - 2}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge m + 3\\x \ge \frac{{3m - 3}}{{m - 2}}\end{array} \right.\)
\( \Rightarrow \) HPT không có nghiệm duy nhất.
Vậy có 1 giá trị của m thỏa mãn yêu cầu đề bài.
Chọn B.
Câu 6:
Phương pháp:
Sắp xếp các số liệu thống kê thành dãy không tăng hoặc không giảm. Số trung vị \({M_e}\) là số đứng giữa dãy nếu số phần tử là lẻ và là trung bình cộng của hai số đứng giữa nếu dãy số phần tử là chẵn.
Cách giải:
Có 6 phần tử là điểm cuẩ các em học sinh nên \({M_e} = \frac{{{x_3} + {x_4}}}{2} = \frac{{7 + 8}}{2} = 7,5.\)
Chọn D.
Câu 7:
Phương pháp:
Áp dụng công thức biến tổng thành tích.
Cách giải:
Ta có: \(\left\{ \begin{array}{l}\cos a - \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array} \right.\)
Vậy D sai.
Chọn D.
Câu 8:
Phương pháp:
Áp dụng công thức: \(\left\{ \begin{array}{l}\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\\\sin \left( {a - b} \right) = \sin a\cos b - \cos a\sin b\end{array} \right..\)
Cách giải:
\(\begin{array}{l}M = \cos \left( {x + \frac{\pi }{4}} \right) + \sin \left( {x - \frac{\pi }{4}} \right)\\ = \cos x\cos \frac{\pi }{4} - \sin x\sin \frac{\pi }{4} \\+ \sin x\cos \frac{\pi }{4} - \cos x\sin \frac{\pi }{4}\\ = \frac{{\sqrt 2 }}{2}\cos x - \frac{{\sqrt 2 }}{2}\sin x \\+ \frac{{\sqrt 2 }}{2}\sin x - \frac{{\sqrt 2 }}{2}\cos x = 0.\end{array}\)
Chọn C.
Câu 9:
Phương pháp:
Xác định dấu của \(\cos x,\sin x\) dựa vào đường tròn lượng giác từ đó tính bởi công thức \({\sin ^2}x + {\cos ^2}x = 1\).
Sử dụng công thức: \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b.\)
Cách giải:
Ta có: \(\frac{\pi }{2} < a < \pi \Rightarrow \cos a < 0\)
\( \Rightarrow \cos a = - \sqrt {1 - {{\sin }^2}a} \)\( = - \sqrt {1 - \frac{{16}}{{25}}} = - \sqrt {\frac{9}{{25}}} = - \frac{3}{5}\)
Ta có: \(0 < b < \frac{\pi }{2} \Rightarrow \sin b > 0\)
\(\begin{array}{l} \Rightarrow \sin b = \sqrt {1 - {{\cos }^2}b} \\ = \sqrt {1 - \frac{{64}}{{289}}} = \sqrt {\frac{{225}}{{289}}} = \frac{{15}}{{17}}\\ \Rightarrow \sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\\ = \frac{4}{5}.\frac{8}{{17}} - \frac{3}{5}.\frac{{15}}{{17}} = - \frac{{13}}{{85}}.\end{array}\)
Chọn A.
Câu 10:
Phương pháp:
Phương trình đường thẳng d có hệ số góc là k có dạng \(y = kx + b\)
Đường thẳng \(ax + by + c = 0\) nhận vecto\(\overrightarrow n = \left( {a;\,\,b} \right)\) làm VTPT, nhận vecto \(\overrightarrow u = \left( { - a;\,\,b} \right) = \left( {a; - b} \right)\) làm VTCP và song song với đường thẳng có phương trình \(ax + by + d = 0\,\,\,\left( {d \ne c} \right).\)
Cách giải:
Đường thẳng \(d:\,\,x + 5y - 2019 = 0\) nhận vecto \(\overrightarrow n = \left( {1;\,\,5} \right)\) làm VTPT và nhận các vecto \(\overrightarrow u = \left( { - 5;\,\,1} \right) = \left( {5; - 1} \right)\) làm VTCP
\( \Rightarrow \) Đáp án A và B đúng.
Ta có: \(d:x + 5y - 2019 = 0\)\( \Leftrightarrow y = - \frac{1}{5}x + \frac{{2019}}{5}\) có hệ số góc là \(k = - \frac{1}{5}\)
\( \Rightarrow \) Đáp án C sai.
Chọn C.
Câu 11:
Phương pháp:
Sử dụng phương trình đoạn chắn để viết phương trình đường thẳng \(AB.\)
Cách giải:
Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm \(A\left( {0;2} \right),\,\,B\left( { - 3;0} \right)\).
Phương trình đường thẳng AB là: \(\frac{x}{{ - 3}} + \frac{y}{2} = 1\)
Chọn B.
Câu 12:
Phương pháp:
Tìm giao điểm của \({d_1},\,\,{d_2}\) sau đó thay tọa độ giao điểm đó vào phương trình đường thẳng \({d_3}\) để tìm m.
Cách giải:
Gọi I là giao điểm của \({d_1},\,\,{d_2}\)
\( \Rightarrow \) Tọa độ I là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}5x - 6y - 4 = 0\\x + 2y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right. \)
\(\Rightarrow I\left( {2;1} \right)\)
Để ba đường thẳng đã cho cùng đi qua một điểm \( \Leftrightarrow I \in {d_3}\)
\( \Leftrightarrow 2m - \left( {2m - 1} \right) + 9m - 19 = 0\) \( \Leftrightarrow 9m - 18 = 0 \Leftrightarrow m = 2\)
Chọn D.
Câu 13:
Phương pháp:
Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right) \Rightarrow {d_{\left( {{M_0};\Delta } \right)}} = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)
Cách giải:
\(\Delta \) cách đều 2 điểm \(A,\,\,B \Leftrightarrow d\left( {A;\Delta } \right) = d\left( {B;\Delta } \right)\)
\(\begin{array}{l} \Leftrightarrow \frac{{\left| {m - 1 + 3} \right|}}{{\sqrt {{m^2} + 1} }} = \frac{{\left| { - 2m - 4 + 3} \right|}}{{\sqrt {{m^2} + 1} }} \\\Leftrightarrow \left| {m + 2} \right| = \left| { - 2m - 1} \right|\\ \Leftrightarrow \left[ \begin{array}{l}m + 2 = - 2m - 1\\m + 2 = 2m + 1\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}3m = - 3\\m = 1\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 1\end{array} \right..\end{array}\)
Chọn C.
Câu 14:
Phương pháp:
Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( {O,R} \right) \Leftrightarrow d\left( {O;\Delta } \right) = R.\)
Cách giải:
Ta có đường tròn \(\left( C \right)\) có tâm \(I\) và tiếp xúc với đường thẳng \(\Delta \)
\( \Rightarrow R = d\left( {I;\Delta } \right) = \frac{{\left| {3.2 + 4.1 - 5} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{5}{5} = 1\)
\( \Rightarrow \) Phương trình đường tròn \(\left( C \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 1.\)
Chọn A.
Câu 15:
Phương pháp:
Phương trình chính tắc của Elip có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({a^2} - {b^2} = {c^2}\)
Trong đó: trục lớn \({A_1}{A_2} = 2a\); trục nhỏ \({B_1}{B_2} = 2b\); tiêu cự \({F_1}{F_2} = 2c\)
Cách giải:
Theo đề bài, elip \(\left( E \right)\) có \(\left\{ \begin{array}{l}2a = 12\\2b = 2c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = c\end{array} \right.\)
\( \Rightarrow {6^2} = {b^2} + {c^2} = 2{b^2} \Leftrightarrow {b^2} = 18\)
\( \Rightarrow \) Phương trình Elip \(\left( E \right)\): \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{18}} = 1\)
Chọn B.
Câu 16:
Phương pháp:
Chứng minh ABOC là hình vuông từ đó tính OA để suy ra m.
Cách giải:
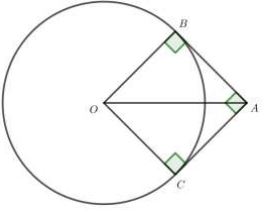
Từ A kẻ 2 tiếp tuyến \(AB,\,\,AC\) với \(\left( C \right)\)
\(\left( C \right)\) có tâm \(O\left( {2; - 1} \right)\) bán kính \(R = 1\)
Tứ giác ABOC có \(\left\{ \begin{array}{l}\angle A = \angle B = \angle C = {90^o}\\OB = OC = R\end{array} \right.\)
\( \Rightarrow \) ABOC là hình vuông (dhnb).
\( \Rightarrow AC = OC = R = 1 \Rightarrow OA = \sqrt 2 \)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {m - 2} \right)}^2} + {{\left( {1 - m + 1} \right)}^2}} = \sqrt 2 \\ \Leftrightarrow 2{\left( {m - 2} \right)^2} = 2 \Leftrightarrow {\left( {m - 2} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 1\\m - 2 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\end{array} \right.\end{array}\)
Chọn A.
II. TỰ LUẬN
Bài 1.
Phương pháp:
a) Giải từng BPT và hợp nghiệm. \(\left| A \right| < B \Leftrightarrow \left\{ \begin{array}{l}B > 0\\{A^2} < {B^2}\end{array} \right..\)
b) \(\sqrt {f\left( x \right)} < g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) > 0\\f\left( x \right) < {g^2}\left( x \right)\end{array} \right.\)
Cách giải:
a) Giải hệ bất phương trình sau trên tập số thực : \(\left\{ \begin{array}{l}\left( {x - 3} \right)\left( {{x^2} - 4x + 4} \right)\left( {{x^2} + x - 2} \right) > 0\\\left| {x - 1} \right| < x + 1\end{array} \right.\)
\(\begin{array}{l}\left( {x - 3} \right)\left( {{x^2} - 4x + 4} \right)\left( {{x^2} + x - 2} \right) > 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {{x^2} + x - 2} \right){\left( {x - 2} \right)^2} > 0\\ \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\\left( {x - 3} \right)\left( {{x^2} + x - 2} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\\left( {x - 3} \right)\left( {x - 1} \right)\left( {x + 2} \right) > 0\end{array} \right.\,\,\,\,\left( I \right)\end{array}\)
Đặt \(f\left( x \right) = \left( {x - 3} \right)\left( {{x^2} + x - 2} \right)\) . Ta có bảng:
\(\begin{array}{l} + )\,\,\,\left| {x - 1} \right| < x + 1\\ \Leftrightarrow \left\{ \begin{array}{l}x + 1 > 0\\{\left( {x - 1} \right)^2} < {\left( {x + 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > - 1\\{x^2} - 2x + 1 < {x^2} + 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > - 1\\4x > 0\end{array} \right. \Leftrightarrow x > 0\,\,\,\left( 2 \right)\end{array}\) \( \Rightarrow \left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\\left[ \begin{array}{l} - 2 < x < 1\\x > 3\end{array} \right.\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l} - 2 < x < 1\\x > 3\end{array} \right.\,\,\,\,\,\,\,\left( 1 \right)\)
Từ (1) và (2) hệ bất phương trình đã cho có nghiệm là : \(\left[ \begin{array}{l}0 < x < 1\\x > 3\end{array} \right..\)
b) Giải bất phương trình sau trên tập số thực : \(\sqrt { - 3{x^2} + 7x - 2} + x < 2\)
\(\begin{array}{l}\sqrt { - 3{x^2} + 7x - 2} + x < 2\\ \Leftrightarrow \sqrt { - 3{x^2} + 7x - 2} < 2 - x\\ \Leftrightarrow \left\{ \begin{array}{l} - 3{x^2} + 7x - 2 \ge 0\\2 - x > 0\\ - 3{x^2} + 7x - 2 < 4 - 4x + {x^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{3} \le x \le 2\\x < 2\\4{x^2} - 11x + 6 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{3} \le x < 2\\\left[ \begin{array}{l}x > 2\\x < \frac{3}{4}\end{array} \right.\end{array} \right. \Leftrightarrow \frac{1}{3} \le x < \frac{3}{4}\end{array}\)
Vậy bất phương trình có tập nghiệm là : \(\frac{1}{3} \le x < \frac{3}{4}.\)
Bài 2.
Phương pháp:
a) Áp dụng các công thức lượng giác biến đổi vế trái bằng về phải.
b) Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\)
- Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a.
- Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a.
- Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\)
Cách giải:
a) Chứng minh đẳng thức: \(\frac{{2{{\sin }^2}\left( {x + \frac{\pi }{4}} \right) - 1}}{{\cot x - \sin x.\cos x}} = 2{\tan ^2}x\) khi các biểu thức đều xác định.
Ta có:
\(\begin{array}{l}VT = \frac{{2{{\sin }^2}\left( {x + \frac{\pi }{4}} \right) - 1}}{{\cot x - \sin x.\cos x}}\\ = \frac{{2{{\left( {\sin x\cos \frac{\pi }{4} + \cos x\sin \frac{\pi }{4}} \right)}^2} - 1}}{{\frac{{\cos x}}{{\sin x}} - \sin x.\cos x}}\\ = \frac{{2{{\left( {\frac{{\sqrt 2 }}{2}\sin x + \frac{{\sqrt 2 }}{2}\cos x} \right)}^2} - 1}}{{\frac{{\cos x}}{{\sin x}} - \sin x.\cos x}}\\ = \frac{{{{\left( {\sin x + \cos x} \right)}^2} - 1}}{{\frac{{\cos x}}{{\sin x}} - \sin x.\cos x}}\\ = \frac{{2\sin x\cos x}}{{\frac{{\cos x}}{{\sin x}} - \sin x.\cos x}}\\ = \frac{{2\sin x}}{{\frac{1}{{\sin x}} - \sin x}} = \frac{{2{{\sin }^2}x}}{{1 - {{\sin }^2}x}}\\ = \frac{{2{{\sin }^2}x}}{{{{\cos }^2}x}} = 2{\tan ^2}x = VP.\end{array}\)
Vậy \(\frac{{2{{\sin }^2}\left( {x + \frac{\pi }{4}} \right) - 1}}{{\cot x - \sin x.\cos x}} = 2{\tan ^2}x.\)
b) Tìm các giá trị của tham số m để bất phương trình \( - 1 \le \frac{{{x^2} - 2x - m}}{{{x^2} + 2x + 2019}} < 2\) nghiệm đúng với mọi số thực x.
\(\begin{array}{l} - 1 \le \frac{{{x^2} - 2x - m}}{{{x^2} + 2x + 2019}} < 2\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 \le \frac{{{x^2} - 2x - m}}{{{x^2} + 2x + 2019}}\\\frac{{{x^2} - 2x - m}}{{{x^2} + 2x + 2019}} < 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - {x^2} - 2x - 2019 \le {x^2} - 2x - m\\{x^2} - 2x - m < 2{x^2} + 4x + 4038\end{array} \right.\\\left( {do\,\,{x^2} + 2x + 2019 > 0\,\,\forall x \in \mathbb{R}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2{x^2} + 2019 - m \ge 0\,\,\,\,\,(1)\\{x^2} + 6x + m + 4038 > 0\,\,\,\,\,(2)\end{array} \right.\end{array}\)
Để bất phương trình nghiệm đúng với mọi số thực \(x\,\, \Leftrightarrow \) (1) và (2) nghiệm đúng với mọi số thực \(x\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\Delta _1} \le 0\\{\Delta _2} < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2\left( {2019 - m} \right) \le 0\\9 - \left( {m + 4038} \right) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2019 - m \ge 0\\ - 4029 - m < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \le 2019\\m > - 4029\end{array} \right.\\ \Leftrightarrow - 4029 < m \le 2019.\end{array}\)
Vậy với \( - 4029 < m \le 2019\) thỏa mãn yêu cầu đề bài.
Bài 3.
Phương pháp:
a) Đường trung trực của đoạn thẳng \(AB\) đi qua trung điểm \(I\) của \(AB\) và nhận vecto \(\overrightarrow {AB} \) làm VTPT.
b) Gọi \(M\left( {m;2m - 5} \right) \in d\) là tâm của đường tròn \(\left( C \right)\), lập phương trình tìm m.
c) Viết phương trình đường thẳng qua tâm M song song với đường thẳng d’ từ đó tìm giao của đường thẳng với đường tròn. Hai điểm đó chính là tiếp điểm của hai tiếp tuyến cần tìm.
Cách giải:
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng \(d:2x - y - 5 = 0\) và hai điểm \(A\left( {1;2} \right),\,\,B\left( {4;1} \right)\)
a) (1 điểm) Viết phương trình đường trung trực đoạn thẳng AB.
Gọi I là trung điểm của AB \( \Rightarrow I\left( {\frac{5}{2};\frac{3}{2}} \right)\)
Gọi \(\Delta \) là đường trung trực của AB \( \Rightarrow I \in \Delta \)
\(\overrightarrow {AB} = \left( {3; - 1} \right)\) là một VTPT của \(\Delta \)
\( \Rightarrow \Delta :3\left( {x - \frac{5}{2}} \right) - \left( {y - \frac{3}{2}} \right) = 0\)\( \Leftrightarrow 3x - y - 6 = 0\)
b) (1 điểm) Viết phương trình đường tròn \(\left( C \right)\) có tâm thuộc đường thẳng d và đi qua 2 điểm A, B.
Gọi \(M\left( {m;2m - 5} \right) \in d\) là tâm của đường tròn \(\left( C \right)\)
Đường tròn \(\left( C \right)\) đi qua \(A,B\)
\(\Rightarrow MA = MB \Leftrightarrow M{A^2} = M{B^2}\)
\(\begin{array}{l} \Leftrightarrow {\left( {1 - m} \right)^2} + {\left( {2 - 2m + 5} \right)^2} \\= {\left( {4 - m} \right)^2} + {\left( {1 - 2m + 5} \right)^2}\\ \Leftrightarrow {\left( {1 - m} \right)^2} - {\left( {4 - m} \right)^2} \\= {\left( {6 - 2m} \right)^2} - {\left( {7 - 2m} \right)^2}\\ \Leftrightarrow - 3\left( {5 - 2m} \right) = - \left( {13 - 4m} \right)\\ \Leftrightarrow 2m = 2 \Leftrightarrow m = 1\\ \Rightarrow M\left( {1; - 3} \right)\end{array}\)
Bán kính của đường tròn \(\left( C \right)\) là \(MA = \sqrt {0 + {5^2}} = 5\)
\( \Rightarrow \) Phương trình đường tròn \(\left( C \right)\): \({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 25.\)
c) (0,5 điểm) Viết phương trình tiếp tuyến của \(\left( C \right)\) biết tiếp tuyến vuông góc với đường thẳng \(d':x + y + 2019 = 0\)
Gọi \(\Delta '\) là đường thẳng qua M song song với d’
\( \Rightarrow \overrightarrow n = \left( {1;1} \right)\) là VTPT của d’ và \(\Delta '\)
\( \Rightarrow \Delta ':\left( {x - 1} \right) + \left( {y + 3} \right) = 0\)\( \Leftrightarrow x + y + 2 = 0\)
Gọi \(N,\,\,P\) là giao điểm của \(\Delta '\) với \(\left( C \right)\)
\( \Rightarrow \) Tọa độ \(N,\,\,P\) là nghiệm của hệ:
\(\begin{array}{l}\left\{ \begin{array}{l}x + y + 2 = 0\\{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 25\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = - y - 2\\{\left( { - y - 3} \right)^2} + {\left( {y + 3} \right)^2} = 25\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = - y - 2\\{\left( {y + 3} \right)^2} = \frac{{25}}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1 - \frac{5}{{\sqrt 2 }}\\y = \frac{5}{{\sqrt 2 }} - 3\end{array} \right.\\ \Rightarrow N\left( {1 - \frac{5}{{\sqrt 2 }};\frac{5}{{\sqrt 2 }} - 3} \right)\\\left\{ \begin{array}{l}x = 1 + \frac{5}{{\sqrt 2 }}\\y = - \frac{5}{{\sqrt 2 }} - 3\end{array} \right. \\\Rightarrow P\left( {1 + \frac{5}{{\sqrt 2 }}; - \frac{5}{{\sqrt 2 }} - 3} \right)\end{array} \right.\end{array}\)
Vì tiếp tuyến cần tìm vuông góc với d’ nên chúng cũng vuông góc với \(\Delta '\)
\( \Rightarrow \) Các tiếp tuyến cần tìm tiếp xúc với đương tròn \(\left( C \right)\) tại \(N,\,\,P\)
\(\overrightarrow {n'} = \left( {1; - 1} \right)\) là VTPT của các tiếp tuyến cần tìm
+) Với tiếp điểm N
\( \Rightarrow \) Phương trình tiếp tuyến \({d_1}:\left( {x - 1 + \frac{5}{{\sqrt 2 }}} \right) - y + \frac{5}{{\sqrt 2 }} - 3 = 0\)\( \Leftrightarrow x - y + \frac{{10}}{{\sqrt 2 }} - 4 = 0\)
+) Với tiếp điểm P
\( \Rightarrow \) Phương trình tiếp tuyến \({d_2}:\left( {x - 1 - \frac{5}{{\sqrt 2 }}} \right) - y - \frac{5}{{\sqrt 2 }} - 3 = 0\)\( \Leftrightarrow x - y - \frac{{10}}{{\sqrt 2 }} - 4 = 0\)
Vậy có hai phương trình tiếp tuyến thỏa mãn bài toán: \(\left[ \begin{array}{l}x - y + \frac{{10}}{{\sqrt 2 }} - 4 = 0\\x - y - \frac{{10}}{{\sqrt 2 }} - 4 = 0\end{array} \right..\)
Bài 4.
Phương pháp:
Chứng minh \(1 + \frac{1}{{\sin A}} \le 1 + \frac{1}{{\sqrt[3]{{\sin A\sin B\sin C}}}}\) từ đó tìm dấu “=” xảy ra để tính các góc của \(\Delta ABC\)
Cách giải:
Tính các góc của \(\Delta ABC\) biết \(\left( {1 + \frac{1}{{\sin A}}} \right)\left( {1 + \frac{1}{{\sin B}}} \right)\left( {1 + \frac{1}{{\sin C}}} \right) \)\(= {\left( {1 + \frac{1}{{\sqrt[3]{{\sin A\sin B\sin C}}}}} \right)^3}\).
\(\begin{array}{l}\left( {1 + \frac{1}{{\sin A}}} \right)\left( {1 + \frac{1}{{\sin B}}} \right)\left( {1 + \frac{1}{{\sin C}}} \right) \\= {\left( {1 + \frac{1}{{\sqrt[3]{{\sin A\sin B\sin C}}}}} \right)^3}\\ \Leftrightarrow \frac{{\left( {\sin A + 1} \right)\left( {\sin B + 1} \right)\left( {\sin C + 1} \right)}}{{\sin A\sin B\sin C}} \\= \frac{{{{\left( {\sqrt[3]{{\sin A\sin B\sin C}} + 1} \right)}^3}}}{{\sin A\sin B\sin C}}\\ \Leftrightarrow \sin A\sin B\sin C\\ + \sin A\sin B + \sin B\sin C + \sin A\sin C \\+ \sin A + \sin B + \sin C + 1\\= \sin A\sin B\sin C \\+ 3\sqrt[3]{{{{\sin }^2}A{{\sin }^2}B{{\sin }^2}C}} \\+ 3\sqrt[3]{{\sin A\sin B\sin C}} + 1\\ \Leftrightarrow \sin A\sin B + \sin B\sin C + \sin A\sin C \\+ \sin A + \sin B + \sin C \\= 3\sqrt[3]{{{{\sin }^2}A{{\sin }^2}B{{\sin }^2}C}} \\+ 3\sqrt[3]{{\sin A\sin B\sin C}}\end{array}\)
Ta có \(A,\,\,B,\,\,C\) là các góc trong tam giác \( \Rightarrow 0 < \sin A,\sin B,\sin C \le 1\)
Áp dụng bất đẳng thức Cô-si ta được:
\(\begin{array}{l}\left\{ \begin{array}{l}\sin A\sin B + \sin B\sin C + \sin A\sin C \\\ge 3\sqrt[3]{{{{\sin }^2}A{{\sin }^2}B{{\sin }^2}C}}\\\sin A + \sin B + \sin C\\ \ge 3\sqrt[3]{{\sin A\sin B\sin C}}\end{array} \right.\\ \Rightarrow \sin A\sin B + \sin B\sin C + \sin A\sin C \\+ \sin A + \sin B + \sin C \\\ge 3\sqrt[3]{{{{\sin }^2}A{{\sin }^2}B{{\sin }^2}C}} \\+ 3\sqrt[3]{{\sin A\sin B\sin C}}\end{array}\)
Dấu “\( = \)” xảy ra \( \Leftrightarrow \sin A = \sin B = \sin C\) mà \(A,\,\,B,\,\,C\) là các góc trong \(\Delta ABC\)
\( \Rightarrow A = B = C = {60^o}\)
Nguồn: Sưu tầm
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề số 4 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10 timdapan.com"