Đề số 2 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10

Đề bài

A. PHẦN TRẮC NGHIỆM (30 câu; 6,0 điểm)

Câu 1: Mệnh đề nào trong các mệnh đề sau đây sai?

A. \(\tan \left( { - \alpha } \right) =  - \tan \alpha \)

B. \(\cot \left( { - \alpha } \right) =  - \cot \alpha \)

C. \(\sin \left( { - \alpha } \right) =  - \sin \alpha \)

D. \(\cos \left( { - \alpha } \right) =  - \cos \alpha \)

Câu 2: Tìm tập nghiệm \(S\) của bất phương trình: \( - 4x + 16 \le 0.\)

A. \(S = \left[ {4; + \infty } \right)\)

B. \(S = \left( { - \infty ; - 4} \right]\)

C. \(S = \left( { - \infty ;4} \right]\)

D. \(S = \left( {4; + \infty } \right)\)

Câu 3: Bảng xét dấu sau là của biểu thức nào?

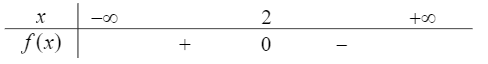
A.\(f\left( x \right) = 2 - 4x\)

B. \(f\left( x \right) = 16 - 8x\)

C. \(f\left( x \right) =  - x - 2\)

D. \(f\left( x \right) = x - 2\)

Câu 4: Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có tọa độ đỉnh \(A\left( {1;2} \right),B\left( {3;1} \right),C\left( {5;4} \right)\). Phương trình nào sau đây là phương trình đường cao của tam giác \(ABC\) kẻ từ \(A.\)

A.\(5x - 6y + 7 = 0\)

B. \(2x + 3y - 8 = 0\)

C. \(3x - 2y - 5 = 0\)

D. \(3x - 2y + 5 = 0\)

Câu 5: Tìm tập nghiệm của bất phương trình: \(2\left( {x - 2} \right)\left( {x - 1} \right) \le x + 13.\)

A. \(\left[ { - 1;\frac{9}{2}} \right]\)

B. \(\left[ { - 2;\frac{9}{4}} \right]\)

C. \(\left[ { - \frac{1}{2};9} \right]\)

D. \(\left[ { - \frac{3}{2};3} \right]\)

Câu 6: Tìm các giá trị của tham số \(m\) để bất phương trình: \(\left( {m - 3} \right){x^2} - 2mx + m - 6 < 0\) có tập nghiệm là \(\mathbb{R}.\)

A. \(2 < m < 3\)

B. \(m < 2\)

C. \(m \le 3\)

D. \(m > 3\)

Câu 7: Trong mặt phẳng \(Oxy\), cho elip \(\left( E \right):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1.\) Tỉ số giữa tiêu cự và độ dài trục lớn của elip bằng:

A. \(\frac{{3\sqrt 5 }}{5}\)

B. \(\frac{{2\sqrt 5 }}{5}\)

C. \(\frac{{\sqrt 5 }}{5}\)

D. \(\frac{{\sqrt 5 }}{4}\)

Câu 8: Trong mặt phẳng \(Oxy\), tọa độ tâm \(I\)  và bán kính \(R\)  của đường tròn \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\) là:

A. \(I\left( {2; - 3} \right),R = 5\)

B. \(I\left( { - 2;3} \right),R = 5\)

C. \(I\left( {2; - 3} \right),R = 25\)

D. \(I\left( { - 2;3} \right),R = 25\)

Câu 9: Trong mặt phẳng \(Oxy\), góc giữa hai đường thẳng \({d_1}:x + 2y + 4 = 0\) và \({d_2}:x - 3y + 6 = 0\)  là:

A. \(30^\circ \)

B. \(60^\circ \)

C. \(45^\circ \)

D. \(23^\circ 12'\)

Câu 10: Trong mặt phẳng \(Oxy\), vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 + 3t\\y =  - 3 - t\end{array} \right.\)

A. \(\overrightarrow u \left( {2; - 3} \right)\)

B. \(\overrightarrow u \left( {3; - 1} \right)\)

C. \(\overrightarrow u \left( {3;1} \right)\)

D. \(\overrightarrow u \left( {3; - 3} \right)\)

Câu 11: Tam giác có ba cạnh lần lượt là \(3;\,\,8;\,\,9.\) Góc lớn nhất của tam giác đó có cosin bằng bao nhiêu?

A. \(\frac{{\sqrt {17} }}{4}\)

B. \( - \frac{4}{{25}}\)

C. \( - \frac{1}{6}\)

D.\(\frac{1}{6}\)

Câu 12: Trong mặt phẳng \(Oxy\), với giá trị nào của \(m\) thì đường thẳng: \({\Delta _1}:\left( {2m - 1} \right)x + my - 10 = 0\) vuông góc với đường thẳng \({\Delta _2}:3x + 2y + 6 = 0.\)

A. \(m = 0\)

B. \(m \in \emptyset \)

C. \(m = 2\)

D. \(m = \frac{3}{8}\)

Câu 13: Người ta dùng \(100m\) rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của hình chữ nhật là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được?

A. \(625{m^2}\)

B. \(1150{m^2}\)

C. \(1350{m^2}\)

D. \(1250{m^2}\)

Câu 14: Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {y^2} + 6x - 2y + 5 = 0\) và điểm \(A\left( { - 4;2} \right).\) Đường thẳng \(d\) đi qua điểm \(A\)  cắt \(\left( C \right)\) tại hai điểm phân biệt \(M,\,\,N\)  sao cho \(A\)  là trung điểm của \(MN\)  có phương trình là:

A. \(7x - y + 30 = 0\)

B. \(7x - y + 35 = 0\)

C. \(x - y + 6 = 0\)

D. \(7x - 3y + 34 = 0\)

Câu 15: Với số thực \(a\) bất kỳ, biểu thức nào sau đây luôn dương?

A. \({a^2} - 2a + 1\)

B. \({a^2} + a + 1\)

C. \({a^2} + 2a + 1\)

D. \({a^2} + 2a - 1\)

Câu 16: Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right)\) có tâm \(I\left( {1;3} \right)\) và đi qua điểm \(M\left( {3;1} \right)\) có phương trình là:

A. \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 8\)

B. \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 10\)     

C. \({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 10\)

D. \({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 8\)

Câu 17: Giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{x}{2} + \frac{2}{{x - 1}}\) với \(x > 1\) là:

A. \(3\)

B. \(2\sqrt 2 \)

C. \(2\)

D.\(\frac{5}{2}\)

Câu 18: Trong mặt phẳng \(Oxy\), khoảng cách từ điểm \(M\left( {2; - 3} \right)\) đến đường thẳng \(\Delta :2x + 3y - 7 = 0\)  là:

A. \(\frac{5}{{\sqrt {13} }}\)

B. \(\frac{{12}}{{13}}\)

C. \(\frac{{12}}{{\sqrt {13} }}\)

D.\(\frac{5}{{13}}\)

Câu 19: Trong tam giác ABC có góc \(\angle A = 60^\circ ;\,\,AC = 10;\,\,AB = 6.\)  Khi đó, độ dài cạnh \(BC\)  là:

A. \(2\sqrt {19} \)

B. \(76\)

C. \(14\)

D. \(6\sqrt 2 \)

Câu 20: Biết \(A,B,C\) là ba góc của tam giác \(ABC,\)  mệnh đề nào sau đây đúng?

A. \(\cos \left( {A + C} \right) =  - \cos B\)

B. \(\tan \left( {A + C} \right) = \tan B\)

C. \(\sin \left( {A + C} \right) =  - \sin B\)

D. \(\cot \left( {A + C} \right) = \cot B\)

Câu 21: Cho \(\cos \alpha  = \frac{4}{{13}},0 < \alpha  < \frac{\pi }{2}.\) Khi đó \(\sin \alpha \) bằng:

A. \(\frac{{ - 3\sqrt {17} }}{{13}}\)

B. \(\frac{4}{{3\sqrt {17} }}\)

C. \(\frac{{3\sqrt {17} }}{{13}}\)

D. \(\frac{{3\sqrt {17} }}{{14}}\)

Câu 22: Tính chu vi tam giác ABC biết \(AB = 6\) và \(2\sin A = 3\sin B = 4\sin C\).

A. \(26\)

B. \(13\)

C. \(5\sqrt {26} \)

D. \(10\sqrt 6 \)

Câu 23: Cho \(\sin \alpha  + \cos \alpha  = \frac{5}{4}.\) Khi đó \(\sin 2\alpha \) có giá trị bằng:

A. \(\frac{5}{2}\)

B. \(2\)

C. \(\frac{3}{{32}}\)

D. \(\frac{9}{{16}}\)

Câu 24: Tìm tập nghiệm của bất phương trình: \(\frac{{2 - x}}{{3x - 2}} \ge 1.\)

A. \(\left( { - \infty ;1} \right]\backslash \left\{ {\frac{2}{3}} \right\}\)

B. \(\left[ {1; + \infty } \right)\)

C. \(\left( { - \infty ;\frac{2}{3}} \right)\)

D. \(\left( {\frac{2}{3};1} \right]\)

Câu 25: Trong mặt phẳng \(Oxy\), phương trình tổng quát của đường thẳng đi qua hai điểm \(A\left( {2;1} \right)\) và \(B\left( { - 1; - 3} \right)\) là:

A. \(4x + 3y - 5 = 0\)

B. \(4x - 3y - 5 = 0\)

C. \(3x + 4y + 5 = 0\)

D. \(3x - 4y - 5 = 0\)

Câu 26: Trong mặt phẳng \(Oxy\), phương trình chính tắc của elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:

A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{{16}} = 1\)

B. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\)

C. \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)

D. \(9{x^2} + 16{y^2} = 1\)

Câu 27: Rút gọn biểu thức \(P = \frac{{\cos a - \cos 5a}}{{\sin 4a + \sin 2a}}\) (với \(\sin 4a + \sin 2a \ne 0\)) ta được:

A. \(P = 2\cot a\)

B. \(P = 2\cos a\)

C. \(P = 2\tan a\)

D. \(P = 2\sin a\)

Câu 28: Tìm các giá trị của tham số \(m\) để bất phương trình: \(mx + 4 > 0\) nghiệm đúng với mọi \(x\) thỏa mãn \(\left| x \right| < 8.\)

A. \(m \in \left[ { - \frac{1}{2};\frac{1}{2}} \right]\)

B. \(m \in \left( { - \infty ;\frac{1}{2}} \right]\)

C. \(m \in \left[ { - \frac{1}{2}; + \infty } \right)\)

D. \(m \in \left[ { - \frac{1}{2};0} \right) \cup \left( {0;\frac{1}{2}} \right]\)

Câu 29: Trong mặt phẳng \(Oxy\), cho elip \(\left( E \right):\frac{{{x^2}}}{4} + {y^2} = 1.\) Xét các điểm \(A\left( {a;b} \right)\) và \(B\) thuộc elip sao cho tam giác \(OAB\) cân cân tại \(O\)  và có diện tích đạt giá trị lớn nhất. Tính tích \(ab\) biết \(a;b\) là hai số dương và điểm \(B\) có hoành độ dương.

A. \(ab = \frac{1}{2}\)

B. \(ab = 3\)

C. \(ab = 1\)

D. \(ab = \frac{1}{3}\)

Câu 30: Tìm các giá trị của tham số \(m\) để phương trình: \({x^2} - 2mx - {m^2} - 3m + 4 = 0\) có hai nghiệm trái dấu.

A. \( - 4 < m < 1\)

B. \(\left[ \begin{array}{l}m <  - 4\\m > 1\end{array} \right.\)

C. \( - 1 < m < 4\)

D. \(\left[ \begin{array}{l}m > 4\\m <  - 1\end{array} \right.\)

B. PHẦN TỰ LUẬN (4,0 điểm)

Bài 1. (2,0 điểm) Giải phương trình và bất phương trình sau:

a) \(\sqrt {{x^2} + 2x - 4}  = 3x - 4.\)  

b) \(\frac{{{x^2} + 7x}}{{{x^2} - 3x + 2}} \ge 1.\)

Bài 2. (2,0 điểm) Trong mặt phẳng tọa độ \(Oxy,\) cho các điểm \(A\left( { - 1;2} \right),B\left( {3;4} \right).\)

a) Lập phương trình của đường tròn \(\left( C \right)\) có đường kính là \(AB.\)

b) Lập phương trình tiếp tuyến với \(\left( C \right)\) tại điểm\(A\left( { - 1;2} \right).\)

c) Lập phương trình của đường thẳng đi qua điểm \(M\left( {0;2} \right)\) và cắt đường tròn \(\left( C \right)\) tại hai điểm phân biệt \(P;Q\) sao cho độ dài đoạn thẳng \(PQ\) đạt giá trị nhỏ nhất.

Lời giải chi tiết

1. D	2. A	3. B	4. B	5. A
6. B	7. C	8. A	9. C	10.  B
11. C	12. D	13. D	14. C	15. B
16. A	17. D	18. C	19. A	20. A
21. C	22. A	23. D	24. D	25. B
26. C	27. D	28. A	29. C	30. B

A. PHẦN TRẮC NGHIỆM (30 câu; 6,0 điểm)

Câu 1 (NB)

Phương pháp:

Quan hệ lượng giác giữa các cung đặc biệt.

Cách giải:

Ta có: \(\cos \left( { - \alpha } \right) = \cos \alpha  \Rightarrow \) D sai.

Chọn D.

Câu 2 (NB)

Phương pháp:

Giải bất phương trình bậc nhất một ẩn.

Cách giải:

\( - 4x + 16 \le 0 \Leftrightarrow 4x \ge 16 \Leftrightarrow x \ge 4.\)

Vậy tập nghiệm của bất phương trình là \(S = \left[ {4; + \infty } \right).\)

Chọn A.

Câu 3 (TH)

Phương pháp:

Dựa vảo bảng xét dấu để nhận xét dấu của biểu thức cần tìm rồi chọn đáp án đúng.

Cách giải:

Từ bảng xét dấu ta suy ra: \(\left\{ \begin{array}{l}f\left( x \right) = 0 \Leftrightarrow x = 2\\f\left( x \right) > 0 \Leftrightarrow x < 2\\f\left( x \right) < 0 \Leftrightarrow x > 2\end{array} \right..\)

Vậy đó là bảng xét dấu của biểu thức \(f\left( x \right) = 16 - 8x.\)

Chọn B.

Câu 4 (TH)

Phương pháp:

Đường cao của tam giác \(ABC\)  kẻ từ \(A\) sẽ nhận \(\overrightarrow {BC} \) là một VTPT.

Phương trình đường thẳng \(d\) đi qua \(M\left( {{x_0};\,\,{y_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;\,\,B} \right)\) có dạng: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) = 0.\)

Cách giải:

Đường cao của \(\Delta ABC\) kẻ từ \(A\left( {1;2} \right)\) sẽ nhận \(\overrightarrow {BC} \left( {2;3} \right)\) là một VTPT nên đường cao đó có phương trình là: \(2\left( {x - 1} \right) + 3\left( {y - 2} \right) = 0 \)

\(\Leftrightarrow 2x + 3y - 8 = 0.\)

Chọn B.

Câu 5 (TH)

Phương pháp:

Giải bất phương trình bằng cách đưa về phương trình tích và sử dụng quy tắc xét dấu của tam thức bậc hai.

Cách giải:

\(\begin{array}{l}2\left( {x - 2} \right)\left( {x - 1} \right) \le x + 13\\ \Leftrightarrow 2{x^2} - 6x + 4 \le x + 13\\ \Leftrightarrow 2{x^2} - 7x - 9 \le 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {2x - 9} \right) \le 0\\ \Leftrightarrow  - 1 \le x \le \frac{9}{2}.\end{array}\)

Chọn A.

Câu 6 (VD)

Phương pháp:

Ta có: \(f\left( x \right) = a{x^2} + bx + c < 0,\) \(\left( {a \ne 0} \right)\forall x \in \mathbb{R} \)

\(\Leftrightarrow \left\{ \begin{array}{l}\Delta  < 0\\a < 0\end{array} \right..\)

Cách giải:

\(\left( {m - 3} \right){x^2} - 2mx + m - 6 < 0\,\,\,\,\left( * \right)\)

Với \(m = 3\) ta có:  \(\left( * \right) \Leftrightarrow  - 6x - 3 < 0 \Leftrightarrow x >  - \frac{1}{2},\) không thỏa mãn.

Với \(m \ne 3,\) để bất phương trình: \(\left( {m - 3} \right){x^2} - 2mx + m - 6 < 0\) có tập nghiệm là \(\mathbb{R}\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - \left( {m - 3} \right)\left( {m - 6} \right) < 0\\m - 3 < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - {m^2} + 9m - 18 < 0\\m < 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}9m - 18 < 0\\m < 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 2\\m < 3\end{array} \right. \\\Leftrightarrow m < 2.\end{array}\)

Chọn B.

Câu 7 (TH)

Phương pháp:

Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có độ dài trục lớn là \(2a,\) độ dài tiêu cự là \(2c = 2\sqrt {{a^2} - {b^2}} .\)

Cách giải:

\(\left( E \right):\,\,\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) có \(a = \sqrt 5 ;\,\,b = 2.\)

\( \Rightarrow \) Độ dài trục lớn là:\(2a = 2\sqrt 5 .\)

\( \Rightarrow \) Độ dài tiêu cự là: \(2c = 2\sqrt {{a^2} - {b^2}}  = 2\sqrt {5 - 4}  = 2.\)

Vậy tỉ số giữa tiêu cự và độ dài trục lớn là: \(\frac{2}{{2\sqrt 5 }} = \frac{{\sqrt 5 }}{5}.\)

Chọn C.

Câu 8 (NB)

Phương pháp:

Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) có tâm \(I\left( {a;b} \right)\) và bán kính \(R.\)

Cách giải:

\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 25\)

\(\Rightarrow I\left( {2; - 3} \right),R = 5.\)

Chọn A.

Câu 9 (TH)

Phương pháp:

Cosin của góc giữa hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\) là:

\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}.\)

Cách giải:

Ta có: \({d_1}:\,\,\,x + 2y + 4 = 0\) có VTPT \(\overrightarrow {{n_1}}  = \left( {1;\,\,2} \right)\) và \({d_2}:\,\,x - 3y + 6 = 0\) có VTPT là: \(\overrightarrow {{n_2}}  = \left( {1; - 3} \right).\)

\( \Rightarrow \cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.1 + 2.\left( { - 3} \right)} \right|}}{{\sqrt {{1^2} + {2^2}} .\sqrt {{1^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}\)

Vậy góc giữa hai đường thẳng \({d_1}:x + 2y + 4 = 0\) và \({d_2}:x - 3y + 6 = 0\) là \(45^\circ .\)

Chọn C.

Câu 10 (NB)

Phương pháp:

Đường thẳng \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) nhận \(\overrightarrow u \left( {a,b} \right)\) là một vectơ chỉ phương.

Cách giải:

Vectơ \(\overrightarrow u \left( {3; - 1} \right)\)là một vectơ chỉ phương của đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 + 3t\\y =  - 3 - t\end{array} \right.\)

Chọn B.

Câu 11 (TH)

Phương pháp:

Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.

Cách giải:

Gọi tam giác đó đã cho là: \(\Delta ABC\,\,\left( {AB = 3,BC = 8,CA = 9} \right)\).

Góc lớn nhất của \(\Delta ABC\) là  \(\angle B\) do \(CA\) là cạnh lớn nhất.

Áp dụng định lý hàm số cos trong \(\Delta ABC\) ta có:

\(C{A^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\) \( \Rightarrow \cos B = \frac{{9 + 64 - 81}}{{2.3.8}} =  - \frac{1}{6}.\)

Chọn C.

Câu 12 (TH)

Phương pháp:

Hai đường thẳng: \({d_1}:\,\,\,{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:\,\,\,{a_2}x + {b_2}y + {c_2} = 0\) vuông góc với nhau

\( \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0 \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} = 0.\)

Cách giải:

\({\Delta _1}:\left( {2m - 1} \right)x + my - 10 = 0\) vuông góc với đường thẳng \({\Delta _2}:3x + 2y + 6 = 0\)

\( \Leftrightarrow \left( {2m - 1} \right).3 + m.2 = 0\) \( \Leftrightarrow 6m - 3 + 2m = 0 \Leftrightarrow m = \frac{3}{8}.\)

Chọn D.

Câu 13 (VD)

Phương pháp:

Sử dụng bất đẳng thức Cauchy.

Cách giải:

Gọi hai cạnh của hình chữ nhật là \(a\) và \(b\) (đơn vị: mét, \(0 < a,b < 100\)).

Giả sử cạnh không phải rào là cạnh  \(b.\)

Vậy số rào cần dùng là \(2a + b = 100\,\left( m \right).\)

Diện tích hình chữ nhật là: \(ab\,\,\,\left( {{m^2}} \right).\)

Áp dụng bất đẳng thức Cauchy cho hai số \(2a,\,\,b\) dương ta có:

\(100 = 2a + b \ge 2\sqrt {2ab}  \Leftrightarrow \sqrt {2ab}  \le 50\)

\(\Leftrightarrow ab \le 1250\,\)

Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}2a = b\\2a + b = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 25\,\,\,\,\left( {tm} \right)\\b = 50\,\,\,\left( {tm} \right)\end{array} \right..\)

Vậy diện tích lớn nhất có thể rào là \(1250\,{m^2}\), khi \(a = 25m,\,\,b = 50m.\) 

Chọn D.

Câu 14 (VD)

Phương pháp:

Tìm tâm và bán kính của đường tròn \(\left( C \right).\)

Vì \(A\) là trung điểm của \(MN\) suy ra \(IA \bot MN.\)

Cách giải:

\(\left( C \right):{x^2} + {y^2} + 6x - 2y + 5 = 0 \)\(\Leftrightarrow \left( C \right):{\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = 5\)

\( \Rightarrow \) Đường tròn \(\left( C \right)\) có tâm \(I\left( { - 3;1} \right)\) và bán kính \(R = \sqrt 5 .\)

Có \(\overrightarrow {IA} \left( { - 1;\,\,1} \right) \Rightarrow IA = \sqrt 2  < \sqrt 5  = R\) nên điểm \(A\) nằm trong đường tròn.

Vì \(A\)  là trung điểm của \(MN \Rightarrow IA \bot MN.\)

Đường thẳng \(MN\) đi qua \(A\left( { - 4;2} \right)\) và nhận \(\overrightarrow {IA} \left( { - 1;1} \right)\) làm một vectơ pháp tuyến có phương trình là:

\( - 1\left( {x + 4} \right) + 1\left( {y - 2} \right) = 0 \)

\(\Leftrightarrow  - x + y - 6 = 0\) \( \Leftrightarrow x - y + 6 = 0.\)

Chọn C.

Câu 15 (TH)

Phương pháp:

Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c > 0\,\,\,\forall x\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  < 0\end{array} \right..\)

Hoặc biến đổi các biểu thức ở đáp án rồi chọn đáp án đúng.

Cách giải:

+) Xét đáp án A: \({a^2} - 2a + 1 = {\left( {a - 1} \right)^2} \ge 0\,\,\,\forall x \Rightarrow \) loại A.

+) Xét đáp án B: \({a^2} + a + 1 = {\left( {a + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0,\forall a \in \mathbb{R}.\)

Chọn B.

Câu 16 (TH)

Phương pháp:

Phương trình đường tròn tâm \(I\left( {a;\,\,b} \right)\) và đi qua điểm \(M\) có bán kính là \(R = IM,\) có phương trình: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = I{M^2}.\)

Cách giải:

 Đường tròn \(\left( C \right)\) có tâm \(I\left( {1;3} \right)\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = {R^2}.\)

\(\left( C \right)\) đi qua điểm \(M\left( {3;1} \right) \Rightarrow {\left( {3 - 1} \right)^2} + {\left( {1 - 3} \right)^2} = {R^2}\)\( \Rightarrow {R^2} = 8.\)

Vậy \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 8.\)

Chọn A.

Câu 17 (VD)

Phương pháp:

Với điều kiện \(x > 1\) ta có: \(\frac{x}{2},\,\,\frac{2}{{x - 1}}\) là các số dương. Biến đổi các biểu thức đã cho và áp dụng bất đẳng thức Cauchy.

Cách giải:

Ta có: \(f\left( x \right) = \frac{x}{2} + \frac{2}{{x - 1}} = \left( {\frac{{x - 1}}{2} + \frac{2}{{x - 1}}} \right) + \frac{1}{2}\)

Với \(x > 1\) ta có: \(\frac{{x - 1}}{2},\,\,\,\frac{2}{{x - 1}}\) là các số dương.

Áp dụng bất đẳng thức Cauchy cho hai số dương \(\frac{{x - 1}}{2},\,\,\,\frac{2}{{x - 1}}\)  ta có:

 \(\begin{array}{l}\frac{{x - 1}}{2} + \frac{2}{{x - 1}} \ge 2\sqrt {\frac{{x - 1}}{2}.\frac{2}{{x - 1}}}  = 2\\ \Rightarrow f\left( x \right) = \frac{{x - 1}}{2} + \frac{2}{{x - 1}} + \frac{1}{2} \ge 2 + \frac{1}{2}\\ \Leftrightarrow f\left( x \right) \ge \frac{5}{2}.\end{array}\)

Dấu “=” xảy ra \( \Leftrightarrow \frac{{x - 1}}{2} = \frac{2}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4\) \( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 2\\x - 1 =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\,\,\,\left( {tm} \right)\\x =  - 1\,\,\,\left( {ktm} \right)\end{array} \right.\)

Vậy giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{x}{2} + \frac{2}{{x - 1}}\) với \(x > 1\) là \(\frac{5}{2}\) khi \(x = 3.\)

Chọn D.

Câu 18 (TH)

Phương pháp:

Cho điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) và đường thẳng \(d:\,\,\,ax + by + c = 0\) ta có: \(d\left( {M;\,\,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)

Cách giải:

Ta có: \(d\left( {M,\,\Delta } \right) = \frac{{\left| {2.2 + 3.\left( { - 3} \right) - 7} \right|}}{{\sqrt {{2^2} + {3^2}} }} = \frac{{12}}{{\sqrt {13} }}.\)

Chọn C.

Câu 19 (TH)

Phương pháp:

Sử dụng hàm số cosin trong tam giác.

Cách giải:

Áp dụng định lý hàm số cos trong \(\Delta ABC\) ta có:

\(\begin{array}{l}B{C^2} \\= A{B^2} + A{C^2} - 2AB.AC.\cos A\\ = 36 + 100 - 2.6.10.\cos 60^\circ  = 76.\\ \Rightarrow BC = 2\sqrt {19} .\end{array}\)

Chọn A.

Câu 20 (NB)

Phương pháp:

Sử dụng quan hệ lương giác giữa các cung đặc biệt.

Cách giải:

Ta có: \(\angle A,\,\,\angle B,\,\,\angle C\) là ba góc trong \(\Delta ABC \Rightarrow \angle A + \angle B + \angle C = {180^0}\)

\( \Rightarrow \cos \left( {A + C} \right) = \cos \left( {180 - B} \right)\)\( =  - \cos B.\)

Chọn A.

Câu 21 (TH)

Phương pháp:

Sử dụng \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\).

Cách giải:

Ta có: \(0 < \alpha  < \frac{\pi }{2} \Rightarrow \sin \alpha  > 0.\)

Có \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \)

\(\Rightarrow \sin \alpha  = \sqrt {1 - {{\cos }^2}\alpha } \)\( = \sqrt {1 - \frac{{16}}{{169}}}  = \frac{{3\sqrt {17} }}{{13}}.\)

Chọn C.

Câu 22 (TH)

Phương pháp:

Chu vi tam giác \(ABC\) là: \(AB + BC + CA.\)

Sử dụng định lý hàm số sin để tính các cạnh của \(\Delta ABC.\)

Cách giải:

Ta có: \(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{CA}}{{\sin B}} \)\(\Rightarrow \left\{ \begin{array}{l}BC = \frac{{\sin A}}{{\sin C}}.AB\\CA = \frac{{\sin B}}{{\sin C}}.AB\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}BC = 2.6 = 12\\CA = \frac{4}{3}.6 = 8\end{array} \right. \)\(\Rightarrow AB + BC + CA = 26.\)

Chọn A.

Câu 23 (TH)

Phương pháp:

Sử dụng công thức: \(\sin 2\alpha  = 2\sin \alpha .\cos \alpha .\)

Cách giải:

Ta có:

\(\begin{array}{l}\sin \alpha  + \cos \alpha  = \frac{5}{4}\\ \Leftrightarrow {\left( {\sin \alpha  + \cos \alpha } \right)^2} = \frac{{25}}{{16}}\\ \Rightarrow 1 + 2\sin \alpha .\cos \alpha  = \frac{{25}}{{16}}\\ \Rightarrow 1 + \sin 2\alpha  = \frac{{25}}{{16}} \Rightarrow \sin 2\alpha  = \frac{9}{{16}}.\end{array}\)

Chọn D.

Câu 24 (TH)

Phương pháp:

Giải bất phương trình trình bằng quy tắc xét dấu của tam thức bậc hai.

Cách giải:

Điều kiện: \(x \ne \frac{2}{3}.\)

\(\begin{array}{l}\frac{{2 - x}}{{3x - 2}} \ge 1 \Leftrightarrow \frac{{2 - x}}{{3x - 2}} - 1 \ge 0\\ \Leftrightarrow \frac{{2 - x - 3x + 2}}{{3x - 2}} \ge 0 \Leftrightarrow \frac{{ - 4x + 4}}{{3x - 2}} \ge 0\\ \Leftrightarrow \frac{{x - 1}}{{3x - 2}} \le 0 \Leftrightarrow \frac{2}{3} < x \le 1.\end{array}\)

Chọn D.

Câu 25 (TH)

Phương pháp:

Tìm vectơ pháp tuyến sau đó viết phương trình đường thẳng.

Cách giải:

\(A\left( {2;1} \right)\) và \(B\left( { - 1; - 3} \right) \Rightarrow \overrightarrow {AB} \left( { - 3; - 4} \right) \Rightarrow AB\) nhận \(\overrightarrow n \left( {4; - 3} \right)\) làm một vectơ pháp tuyến.

Phương trình tổng quát của đường thẳng \(AB\) là: \(4\left( {x - 2} \right) - 3\left( {y - 1} \right) = 0 \)\(\Leftrightarrow 4x - 3y - 5 = 0.\)

Chọn B.

Câu 26 (TH)

Phương pháp:

Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có độ dài trục lớn bằng \(2a\) , độ dài trục nhỏ bằng \(2b.\)

Cách giải:

Độ dài trục lớn của elip là \(8 \Rightarrow 2a = 8 \Leftrightarrow a = 4.\)

Độ dài trục lớn của elip là \(6 \Rightarrow 2b = 6 \Leftrightarrow b = 3.\)

Phương trình chính tắc của elip đã cho là: \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1 \Leftrightarrow \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1.\)

Chọn C.

Câu 27 (TH)

Phương pháp:

Sử dụng các công thức: \(\left\{ \begin{array}{l}\cos a - \cos b =  - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin 2a = 2\sin a\cos a\end{array} \right..\)

Cách giải:

\(\begin{array}{l}P = \frac{{\cos a - \cos 5a}}{{\sin 4a + \sin 2a}} = \frac{{ - 2\sin 3a.\sin \left( { - 2a} \right)}}{{2\sin 3a.\cos a}}\\ = \frac{{ - \sin \left( { - 2a} \right)}}{{\cos a}} = \frac{{\sin 2a}}{{\cos a}} = \frac{{2\sin a.\cos a}}{{\cos a}} \\= 2\sin a.\end{array}\)

Chọn D.

Câu 28 (VD)

Phương pháp:

Chia các trường hợp \(m > 0,m < 0,m = 0\) để biện luận bất phương trình sau đó kết hợp nghiệm.

Cách giải:

Ta có: \(\left| x \right| < 8 \Leftrightarrow  - 8 < x < 8.\)

\(mx + 4 > 0\,\,\,\,\,\,\left( 1 \right).\)

Với \(m > 0 \Rightarrow \left( 1 \right) \Leftrightarrow x > \frac{{ - 4}}{m}.\)

Để bất phương trình nghiệm đúng với mọi \(x\) thỏa mãn \( - 8 < x < 8\) thì \(\frac{{ - 4}}{m} \le  - 8 \Leftrightarrow m \le \frac{1}{2}.\)

Vậy \(0 < m \le \frac{1}{2}\) thỏa mãn.

Với \(m < 0 \Rightarrow \left( 1 \right) \Leftrightarrow x < \frac{{ - 4}}{m}.\)

Để bất phương trình nghiệm đúng với mọi \(x\) thỏa mãn \( - 8 < x < 8\) thì \(\frac{{ - 4}}{m} \ge 8 \Leftrightarrow m \ge  - \frac{1}{2}.\)

Vậy \( - \frac{1}{2} \le m < 0\) thỏa mãn.

Với \(m = 0 \Rightarrow \) \(\left( 1 \right) \Leftrightarrow 4 > 0,\) luôn đúng với mọi \(x.\) Thỏa mãn.

Vậy tập hợp tất cả các giá trị của \(m\) thỏa mãn yêu cầu đề bài là \(\left[ {\frac{{ - 1}}{2};\frac{1}{2}} \right].\)

Chọn A.

Câu 29 (VD)

Phương pháp:

Sử dụng bất đẳng thức Cauchy.

Cách giải:

Vì \(a,b > 0\) nên điểm \(A\) nằm ở góc phần tư thứ nhất.

Tam giác OAB cân và điểm B có hoành độ dương nên điểm B đối xứng với điểm A qua trục hoành, hay \(B\left( {a; - b} \right).\)

Diện tích tam giác OAB là: \(\frac{1}{2}.a.2b = ab.\)

Vì A thuộc elip nên: \(\frac{{{a^2}}}{4} + {b^2} = 1.\)

Theo Cauchy ta có: \(\frac{{{a^2}}}{4} + {b^2} \ge 2\sqrt {\frac{{{a^2}}}{4}.{b^2}}  = ab \Rightarrow ab \le 1.\)

Vậy diện tích tam giác OAB lớn nhất là \(1\)  khi \(a = \sqrt 2 ,b = \frac{{\sqrt 2 }}{2}.\)

Vậy khi đó \(ab = 1.\)

Chọn C.

Câu 30 (TH)

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0.\)

Cách giải:

\({x^2} - 2mx - {m^2} - 3m + 4 = 0\)

Phương trình có hai nghiệm trái dấu \( \Leftrightarrow 1.\left( { - {m^2} - 3m + 4} \right) < 0 \)

\(\Leftrightarrow {m^2} + 3m - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 1\\m <  - 4\end{array} \right..\)

Chọn B.

B. PHẦN TỰ LUẬN (4,0 điểm)

Câu 1 (VD):

Phương pháp:

a) \(\sqrt A  = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right..\)

b) Quy đồng giải bất phương trình tích.

Cách giải:

Giải phương trình và bất phương trình sau:

a) \(\sqrt {{x^2} + 2x - 4}  = 3x - 4\)

Điều kiện: \(x \in \left( { - \infty ; - 1 - \sqrt 5 } \right] \cup \left[ { - 1 + \sqrt 5 ; + \infty } \right).\)

\(\sqrt {{x^2} + 2x - 4}  = 3x - 4 \)

\(\Leftrightarrow \left\{ \begin{array}{l}3x - 4 \ge 0\\{x^2} + 2x - 4 = 9{x^2} - 24x + 16\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\8{x^2} - 26x + 20 = 0\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\\left( {x - 2} \right)\left( {4x - 5} \right) = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\\left[ \begin{array}{l}x - 2 = 0\\4x - 5 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{4}{3}\\\left[ \begin{array}{l}x = 2\\x = \frac{5}{4}\end{array} \right.\end{array} \right. \)

\(\Leftrightarrow x = 2\,\,\,\left( {tm} \right)\)

Vậy \(x = 2\) là nghiệm duy nhất của phương trình.

b) \(\frac{{{x^2} + 7x}}{{{x^2} - 3x + 2}} \ge 1\)

Điều kiện: \(x \ne 1,x \ne 2.\)

\(\frac{{{x^2} + 7x}}{{{x^2} - 3x + 2}} \ge 1 \Leftrightarrow \frac{{{x^2} + 7x - \left( {{x^2} - 3x + 2} \right)}}{{{x^2} - 3x + 2}} \ge 0\)\( \Leftrightarrow \frac{{10x - 2}}{{\left( {x - 1} \right)\left( {x - 2} \right)}} \ge 0\)

Ta có bảng xét dấu:

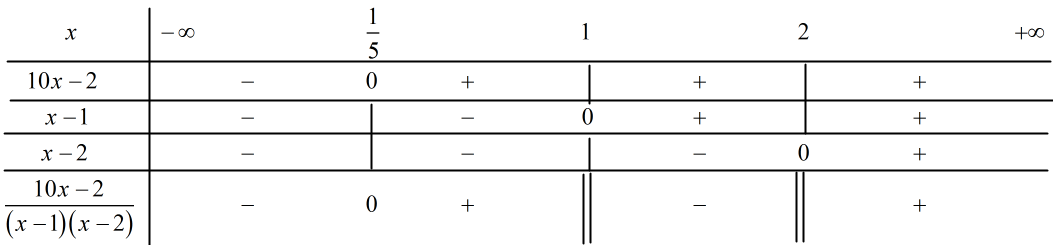
Vậy tập nghiệm của bất phương trình là \(S = \left[ {\frac{1}{5};1} \right) \cup \left( {2; + \infty } \right).\)

Câu 2 (VD)

Phương pháp:

a) Đường tròn đường kính \(AB\) có tâm \(I\) là trung điểm của \(AB\) và bán kính \(R = \frac{{AB}}{2}.\)

b) Tiếp tuyến của \(\left( C \right)\) tại điểm \(A\) nhận \(\overrightarrow {IA} \) làm VTPT với \(I\) là tâm của đường tròn \(\left( C \right).\)

c) Ta có đường thẳng \(d\) cắt  đường tròn \(\left( C \right)\) tại hai điểm phân biệt \(P,\,\,Q\) sao cho \(PQ\) nhỏ nhất \( \Leftrightarrow d\left( {I;\,\,d} \right)\) nhỏ nhất.

Khi đó: \(d\left( {I;\,\,d} \right) = IM.\)

Cách giải:

Trong mặt phẳng tọa độ \(Oxy,\) cho các điểm \(A\left( { - 1;2} \right),B\left( {3;4} \right).\)

a) Lập phương trình của đường tròn \(\left( C \right)\) có đường kính là \(AB.\)

Gọi \(I\) là trung điểm của \(AB \Rightarrow I\left( {1;\,\,3} \right).\)

Ta có: \(AB = \sqrt {{{\left( {3 + 1} \right)}^2} + {{\left( {4 - 2} \right)}^2}}  = 2\sqrt 5 \)\( \Rightarrow R = \frac{{AB}}{2} = \sqrt 5 .\)

\( \Rightarrow \) Phương trình của đường tròn \(\left( C \right)\) có đường kính là \(AB:{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 5.\)

b) Lập phương trình tiếp tuyến với \(\left( C \right)\) tại điểm\(A\left( { - 1;2} \right).\)

Có \(\overrightarrow {IA} \left( { - 2; - 1} \right)\).

Tiếp tuyến với \(\left( C \right)\) tại điểm\(A\left( { - 1;2} \right)\) đi qua \(A\) và nhận \(\overrightarrow {IA} \left( { - 2; - 1} \right)\) là một VTPT nên có phương trình là:

\( - 2\left( {x + 1} \right) - 1\left( {y - 2} \right) = 0 \Leftrightarrow 2x + y = 0.\)

c) Lập phương trình của đường thẳng đi qua điểm \(M\left( {0;2} \right)\) và cắt đường tròn \(\left( C \right)\) tại hai điểm phân biệt \(P;Q\) sao cho độ dài đoạn thẳng \(PQ\) đạt giá trị nhỏ nhất.

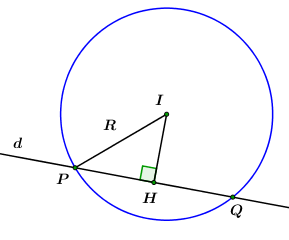
Ta có: \(M\left( {0;2} \right) \Rightarrow IM = \sqrt 2  < R\) nên \(M\) nằm trong đường tròn.

Gọi \(H\) là trung điểm của \(PQ \Rightarrow ID \bot PQ = \left\{ H \right\}\)

\( \Rightarrow PQ = 2IP = 2\sqrt {{R^2} - I{H^2}} \)

\( \Rightarrow PQ\,\,\,Min \Leftrightarrow IH\,\,\,Min \Leftrightarrow H \equiv M \)

\(\Leftrightarrow IH = IM\)

Khi đó  \(PQ\) đi qua \(M\left( {0;2} \right)\) và nhận \(\overrightarrow {MI} \left( {1;1} \right)\) là một vectơ pháp tuyến \( \Rightarrow PQ:1\left( {x - 0} \right) + 1\left( {y - 2} \right) = 0 \)

\(\Leftrightarrow x + y - 2 = 0.\)

Nguồn: Sưu tầm