Đề số 2 - Đề kiểm tra học kì 2 - Toán 6

Đề bài

Bài 1. (2,0 điểm)

Tính giá trị của các biểu thức:

a) \(A =  - \,4 + 19 - 18\)

b) \(B = 2018.17 - 7.2018.\)

c) \(C =  - \dfrac{1}{2} + \dfrac{1}{3} \)       

d) \(D = \dfrac{1}{2} \cdot \dfrac{{250}}{{17}} + \dfrac{1}{2} \cdot \dfrac{{90}}{{17}} \cdot \)

Bài 2. (2,5 điểm)

a) Tìm giá trị của x biết \(2\left( {x - 3} \right) =  - 12.\)

b) Tìm giá trị của x biết \(\,\dfrac{1}{2}\, + 2x = \,\dfrac{5}{6}:\dfrac{2}{3} \cdot \)

c) Tìm x nguyên để các phân số sau là số nguyên \(\dfrac{{13}}{{x - 15}} \cdot \)

Bài 3. (2,5 điểm)

a) Tìm x để giá trị phân số \(\dfrac{{x - 12}}{4}\) và phân số \(\dfrac{1}{2}\) bằng nhau.

b) Tìm giá trị nguyên của x thỏa mãn điều kiện \(1 < \dfrac{x}{3} < 2.\)

c) Một lớp có 45 học sinh làm bài kiểm tra. Số bài lớp đó đạt điểm giỏi bằng \(\dfrac{1}{3}\) tổng số bài. Số bài đạt điểm khá bằng \(\dfrac{9}{{10}}\) số bài còn lại. Tính số bài đạt điểm trung bình, biết rằng lớp đó không có bài được điểm yếu và điểm kém.

Bài 4. (2,0 điểm)

Trên cùng một nửa mặt phẳng bờ chứa tia OA, vẽ tia OB sao cho góc AOB = 55⁰, vẽ tia OC sao cho góc AOC = 110⁰

a) Tính số đo góc BOC.

b) Vẽ tia OB’ là tia đối của tia OA. Tính số đo góc BOB’.

Bài 5. (1,0 điểm)

a) Tính \(\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2018.2019}}\)

b) Cho 2018 số tự nhiên là \({a_1};\,\,{a_2};\,\,{a_3};\,...;\,\,{a_{2018}}\) đều là các số lớn hơn 1 thỏa mãn điều kiện \(\dfrac{1}{{a_1^2}} + \dfrac{1}{{a_2^2}} + \dfrac{1}{{a_3^2}} + ... + \dfrac{1}{{a_{2018}^2}} = 1\). Chứng minh rằng trong 2018 số này, ít nhất sẽ có 2 số bằng nhau.

Lời giải chi tiết

Bài 1:

a) \(A = 15 - 18\)

     \(A =  - 3\)

b) \(B = 2018\left( {17 - 7} \right) = 2018.10\)

    \(B = 20180\)

c) \(C = \dfrac{{ - 3}}{6} + \dfrac{2}{6}\)

    \(C =  - \dfrac{1}{6}\)

d) \(D = \dfrac{1}{2}\left( {\dfrac{{250}}{{17}} + \dfrac{{90}}{{17}}} \right) = \dfrac{1}{2} \cdot \dfrac{{340}}{{17}}\)

   \(D = \dfrac{1}{2} \cdot 20 = 10\)

Bài 2: 

a) \(x - 3 =  - 12:2\)

    \(x - 3 =  - 6\)

    \(x =  - 6 + 3\)

Vậy         \(x =  - 3\)

b) \(\dfrac{1}{2} + 2x = \dfrac{5}{4}\)

     \(2x = \dfrac{5}{4} - \dfrac{1}{2}\)

    \(x = \dfrac{3}{4}:2\)

Vậy \(x = \dfrac{3}{8}\)

c) \(\dfrac{{13}}{{x - 15}}\)  là số nguyên khi \(x - 15\) là ước của 13

\(x - 15 \in \left\{ { \pm 1;\,\, \pm 13} \right\} \)

\(\Rightarrow x \in \left\{ {16;\,\,14;\,\,26;\,\,2} \right\}.\)

Bài 3:

a) \(\dfrac{{x - 12}}{4} = \dfrac{1}{2}\)

     \(\left( {x - 12} \right).2 = 4.1\)

    \(2x - 24 = 4\)

Vậy \(x = 14.\)

b) Do  \(1 < \dfrac{x}{3} < 2 \Rightarrow \dfrac{3}{3} < \dfrac{x}{3} < \dfrac{6}{3}\) nên \(3 < x < 6\)

Vì x là số nguyên nên \(x = 4;\,\,x = 5\)

Vậy có hai giá trị tìm được là \(x = 4;\,\,x = 5\)

c) Số bài loại Giỏi là: \(45.\dfrac{1}{3} = 15\) bài

Số bài loại Khá là \(\dfrac{9}{{10}}\left( {45 - 15} \right) = 27\) bài

Số bài loại Trung Bình \(45 - 15 - 27 = 3\) bài

Bài 4:

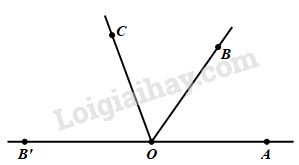
a) Trên cùng nửa mặt phẳng, bờ là đường thẳng chứa OA, ta thấy

\(\widehat {AOB} < \widehat {AOC}\) do \(\left( {{{55}^0} < {{110}^0}} \right)\)

Nên tia OB nằm giữa tia OA và tia OC

Vì thế \(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\)

Thay số: \({55^o} + \widehat {BOC} = {110^o} \Rightarrow \widehat {BOC} = {55^o}\)

b) Vì tia OB’ là tia đối của tia OA nên góc AOB là góc bẹt

Suy ra tia OB nằm giữa tia OA và tia OB’

Suy ra \(\widehat {AOB} + \widehat {BOB}' = \widehat {AOB}'\)

Thay số: \({55^o} + \widehat {BOB}' = {180^o}\)

                        \(\widehat {BOB}' = {125^o}\)

Bài 5:

a) \(\begin{array}{l}\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2018.2019}}\\ = \dfrac{1}{1} - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + .... \\\;\;\;\;+ \dfrac{1}{{2018}} - \dfrac{1}{{2019}}\\ = 1 - \dfrac{1}{{2019}}\end{array}\)

b) Giả sử trong 2018 số đó chẳng có số nào bằng nhau và tất cả các số đều lớn hơn 1. Thế thì:

\(\dfrac{1}{{a_1^2}} + \dfrac{1}{{a_2^2}} + \dfrac{1}{{a_3^2}} + ... + \dfrac{1}{{a_{2018}^2}} \)\(\,\le \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2019}^2}}}\)

Cơ mà:

\(\dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2019}^2}}} \)\(\,< \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2018.2019}}\)

\( = 1 - \dfrac{1}{{2019}} < 1\) (theo phần a)

Thế nhưng đề bài cho \(\dfrac{1}{{a_1^2}} + \dfrac{1}{{a_2^2}} + \dfrac{1}{{a_3^2}} + ... + \dfrac{1}{{a_{2018}^2}} = 1\) (vô lý)

Vậy thể nào trong 2018 số tự nhiên đó cũng có 2 số bằng nhau.