Đề kiểm tra giữa học kì 1 Vật lí 10 - Đề số 03 có lời giải chi tiết

Đề bài

Câu 1: Một hành khách ngồi trong toa A nhìn qua cửa sổ thấy toa B bên cạnh và gạch lát sân ga đều chuyển động như nhau. Khẳng định nào sau đây là đúng?

A. Tàu B chạy, tàu A đứng yên

B. Tàu A chạy, tàu B đứng yên

C.  Cả hai tàu đều chạy

D. Cả hai tàu đều đứng yên

Câu 2: Một chất điểm chuyển động tròn đều với chu kì T, bán kính quỹ đạo R. Công thức tính gia tốc hướng tâm của vật là:

A. \(a = 4{\pi ^2}\frac{{{R^2}}}{{{T^2}}}\) 

B. \(a = 4\pi \frac{R}{{{T^2}}}\)

C. \(a = 4{\pi ^2}\frac{R}{{{T^2}}}\)

D. \(a = 4{\pi ^2}\frac{R}{T}\)

Câu 3: Một chất điểm đứng yên dưới tác dụng của ba lực 12N, 15N, 9N. Góc giữa hai lực 12N và 9N là:

A. \(\alpha  = {30^0}\)            B. \(\alpha  = {60^0}\) 

C. \(\alpha  = {45^0}\)            D. \(\alpha  = {90^0}\)

Câu 4: Một chiếc ca nô chạy thẳng đều xuôi theo dòng chảy từ bến A đến bến B phải mất 1 giờ và khi chạy ngược dòng chảy từ bến B trở về bến A phải mất 2 giờ. Nếu canô tắt máy và thả trôi theo dòng chảy từ bến A đến bến B thì phải mất:

A. 4h               B. 2h  

C. 0,5h            D. 3h

Câu 5: Một lực \(\overrightarrow F \) có độ lớn 12N được phân tích thành hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \). Biết \(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right) = {150^0}\) và độ lớn \(\overrightarrow {{F_2}} \) lớn nhất. Độ lớn các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) lần lượt là:

A. \(8\sqrt 3 N;24N\) 

B. \(8\sqrt 3 N;4\sqrt 3 N\) 

C. \(4\sqrt 3 N;8\sqrt 3 N\)

D. \(12\sqrt 3 N;24N\)

Câu 6: Hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) hợp với nhau góc \(\alpha \) thì độ lớn của hợp lực \(\overrightarrow F \) tính theo công thức:

A. \({F^2} = F_1^2 + F_2^2 - 2{F_1}{F_2}\) 

B. \(F_1^2 = {F^2} + F_2^2 + 2F{F_2}.\cos \alpha \)

C. \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha \)

D. \({F^2} = F_1^2 + F_2^2 - 2{F_1}{F_2}.\cos \alpha \)

Câu 7: Gọi \({F_1},{F_2}\) là độ lớn của hai lực thành phần. Khẳng định nào sau đây là đúng khi nói về độ lớn hợp lực F của \({F_1},{F_2}\).

A. Trong mọi trường hợp F luôn luôn lớn hơn F₁ và F₂

B. F không bao giờ nhỏ hơn F₁ và F₂

C. Trong mọi trường hợp, F thỏa mãn \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)

D. F không bao giờ bằng F₁ hoặc F₂.

Câu 8: Một vật được thả rơi tự do từ độ cao h xuống đất ở nơi có gia tốc trọng trường g. Vận tốc của vật ngay trước khi chạm đất là:

A. 2gh             B. \(\sqrt {2gh} \)

C. \(\sqrt {gh} \)          D. gh

Câu 9: Một vật rơi tự do không vận tốc đầu từ độ cao 80m xuống đất. Lấy g = 10m/s². Thời gian vật rơi đến đất là:

A. 3s                B. 1s   

C. 2s                D. 4s

Câu 10: Gia tốc hướng tâm của một chất điểm chuyển động tròn đều thay đổi thế nào nếu tăng tốc độ góc lên 3 lần và giảm bán kính quỹ đạo đi 3  lần?

A. Tăng 9/2 lần           B. Tăng 3 lần 

C. Giảm 3 lần              D. Tăng 1/3 lần

Câu 11: Kim giờ của một đồng hồ dài 3cm, kim phút dài 4cm. Tỉ số tốc độ dài của điểm đầu kim giờ và kim phút là:

A. \(\dfrac{{{v_p}}}{{{v_h}}} = 12\) 

B. \(\dfrac{{{v_p}}}{{{v_h}}} = 16\)

C. \(\dfrac{{{v_h}}}{{{v_p}}} = 16\)

D. \(\dfrac{{{v_h}}}{{{v_p}}} = 12\)

Câu 12: Hai vật có khối lượng \({m_1} < {m_2}\) được thả rơi tự do tại cùng một vị trí (gọi \({t_1},{t_2}\) tương ứng là thời gian tính từ lúc bắt đầu rơi đến lúc chạm đất của vật thứ nhất và vật thứ hai) thì:

A. \({t_1} = {t_2}\)      B. \({t_1} > {t_2}\)

C. \({t_1} < {t_2}\)      D. Không có cơ sở để kết luận

Câu 13: Câu nào dưới đây nói về chuyển động rơi tự do với vận tốc ban đầu bằng 0 là không đúng?

A. Vận tốc tăng dần theo thời gian

B. Khoảng thời gian để vật rơi hết độ cao h là \(t = \sqrt {\frac{{2h}}{g}} \)

C. Chiều chuyển động là chiều từ trên xuuống dưới

D. Gia tốc rơi tự do tại mọi điểm trên Trái đất đều như nhau.

Câu 14: Ở cùng một độ cao với vật A người ta thả vật B rơi sau vật A một thời gian 0,1s. Sau bao lâu kể từ lúc thả vật A thì khoảng cách giữa chúng là 1m? Lấy g = 10m/s².

A. 5,01s           B. 10,05s 

C. 0,105s         D. 1,05s

Câu 15: Một vật rơi tự do từ một độ cao h. Biết rằng trong giấy cuối cùng vật rơi được 35m. Lấy g = 10m/s². Thời gian từ lúc bắt đầu rơi đến lúc chạm đất là:

A. 4s                B. 2s  

C. 6s                D. 1,5s

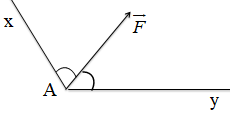
Câu 16: Một lực \(\overrightarrow F \) có độ lớn 15N, điểm đặt lực tại A. Phân tích lực \(\overrightarrow F \) thành hai vecto lực thành phần \(\overrightarrow {{F_x}} \) và \(\overrightarrow {{F_y}} \) theo các phương Ax và Ay như hình vẽ. Giá trị của Fx và Fy là:

 

A. \({F_x} = 7,5N;{F_y} = 7,5\sqrt 3 N\)

B. \({F_x} = 15N;{F_y} = 15N\)

C. \({F_x} = 7,5\sqrt 3 N;{F_y} = 7,5N\)

D. \({F_x} = 7,5N;{F_y} = 7,5N\)

Câu 17: Một chất điểm chuyển động tròn đều trong 60 giây quay được 120 vòng. Chu kì quay của chất điểm là:

A. 0,5s             B. 7200s 

C. 2s                D. 0,2s

Câu 18: Điều nào sáu đây là sai khi nói về chuyển động tròn đều:

A. Tốc độ góc không đổi theo thời gian

B. Tốc độ dài không đổi theo thời gian

C. Vecto vận tốc thay đổi cả về hướng và độ lớn

D. Vecto gia tốc luôn hướng vào tâm quỹ đạo

Câu 19: Một chiếc thuyền chuyển động thẳng đều, ngược chiều dòng nước với vận tốc 6,5km/h đối với dòng nước. Vận tốc chảy của dòng nước đối với bờ sông là 1,5km/h. Vận tốc của thuyền đối với bờ sông:

A. 5 km/h        B. 8 km/h 

C. 6,7 km/h     D. 6,3 km/h

Câu 20: Một vệ tinh nhân tạo chuyển động tròn đều xung quanh Trái đất với tốc độ 8 km/s ở độ cao 600.10³ m (so với mặt đất). Biết bán kính Trái đất là 6400 km. Lấy \(\pi  = 3,14\). Chu kì của vệ tinh là:

A. 84h18ph                 B. 92h03ph

C. 1h31ph35s              D. 1h23ph44s 

Lời giải chi tiết

1.B	2.C	3.D	4.A	5.D	6.C	7.C	8.B	9.D	10.B
11.B	12.A	13.D	14.D	15.A	16.B	17.A	18.C	19.A	20.C

Câu 1:

Chọn B

Câu 2:

Ta có:

\(\left\{ \begin{array}{l}a = \frac{{{v^2}}}{R}\\v = R\omega  = R.\frac{{2\pi }}{T}\end{array} \right.\\ \Rightarrow a = \frac{{{{\left( {2\pi R} \right)}^2}}}{{{T^2}}}.\frac{1}{R} = 4{\pi ^2}\frac{R}{{{T^2}}}\)

Chọn C

Câu 3:

Chất điểm đứng yên => 3 lực đang ở trạng thái cân bằng.

Ta có: hợp lực F=15N

Suy ra:

\(\begin{array}{l}{15^2} = {12^2} + {9^2} + 2.12.9.\cos \alpha \\ \Rightarrow \cos \alpha  = 0 \Rightarrow \alpha  = {90^0}\end{array}\)

Chọn D

Câu 4:

Gọi vật 1 là canô, vật 2 là nước, vật 3 là bờ.

Khi canô chạy xuôi theo dòng nước:

\({v_{12}} + {v_{23}} = \frac{s}{{{t_x}}}\) (1)

Khi canô chạy ngược dòng nước:

\({v_{12}} - {v_{23}} = \frac{s}{{{t_n}}}\) (2)

Từ (1) và (2) suy ra:

\({v_{23}} = \frac{1}{2}\left( {\frac{s}{{{t_x}}} - \frac{s}{{{t_n}}}} \right) = \frac{{s\left( {{t_n} - {t_x}} \right)}}{{2.{t_x}.{t_n}}}\) (3)

Nếu canô tắt máy và thả trôi theo dòng chảy thì:

\(t = \frac{s}{{{v_{23}}}}\) (4)

Thay (3) vào (4) ta được:

\(t = \frac{{2{t_x}{t_n}}}{{{t_n} - {t_x}}} = \frac{{2.1.2}}{{2 - 1}} = 4h\)

Chọn A

Câu 5:

Ta có:

\(\begin{array}{l}{12^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos {150^0}\\ \Leftrightarrow 144 = F_1^2 + F_2^2 - \sqrt 3 {F_1}{F_2}\end{array}\) (1)

Theo đề bài thì độ lớn F2 là lớn nhất => loại B,C

Thay \({F_1} = 8\sqrt 3 ;{F_2} = 24\) vào (1) ta được \(144 \ne 192\) => loại A

Vậy \({F_1} = 12\sqrt 3 N;{F_2} = 24N\)

Chọn D

Câu 6:

Ta có: \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha \)

Chọn C

Câu 7:

Ta có: \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)

Chọn C

Câu 8:

Vận tốc của vật ngay trước khi chạm đất là:

\(v = \sqrt {2gh} \)

Chọn B

Câu 9:

\(h = \frac{1}{2}g{t^2} = t = \sqrt {\frac{{2h}}{g}}  = \sqrt {\frac{{2.80}}{{10}}}  = 4{\rm{s}}\)

Chọn D

Câu 10:

Ta có:

Gia tốc hướng tâm:

\(\left\{ \begin{array}{l}{a_1} = \frac{{{v^2}}}{r} = \frac{{{{\left( {r\omega } \right)}^2}}}{r} = r{\omega ^2}\\{a_2} = \frac{r}{3}.{\left( {3\omega } \right)^2} = 3{\rm{r}}{\omega ^2}\end{array} \right.\\ \Rightarrow \frac{{{a_1}}}{{{a_2}}} = \frac{1}{3} \Rightarrow {a_2} = 3{{\rm{a}}_1}\)

=> gia tốc tăng 3 lần.

Chọn B

Câu 11:

Chu kì của kim giờ là:

\({T_h} = 12h = 43200{\rm{s}}\)

Tốc độ dài của điểm đầu kim giờ là:

\({v_h} = {r_h}\omega  = {r_h}.\frac{{2\pi }}{T} = 0,03.\frac{{2\pi }}{{43200}} \\= 4,{36.10^{ - 6}}m/s\)

Chu kì của kim phút là:

\({T_{ph}} = 3600{\rm{s}}\)

Tốc độ dài của đầu kim phút là:

\({v_{ph}} = {r_{ph}}\omega  = {r_{ph}}.\frac{{2\pi }}{T} = 0,04.\frac{{2\pi }}{{3660}} \\= 6,{98.10^{ - 5}}m/s\)

Suy ra:

\(\frac{{{v_{ph}}}}{{{v_h}}} \approx 16\)

Chọn B

Câu 12:

Ta có: \(t = \sqrt {\frac{{2h}}{g}} \) => thời gian rơi tự do không phụ thuộc vào khối lượng.

Hai vật được thả tại cùng một vị trí nên \({t_1} = {t_2}\).

Chọn A

Câu 13:

Chọn D

Câu 14:

Ta có:

\(\left\{ \begin{array}{l}{y_A} = \frac{1}{2}g{t^2}\\{y_B} = \frac{1}{2}g{\left( {t + 0,1} \right)^2}\end{array} \right.\)

Khoảng cách giữa chúng là 1m, suy ra:

\(\begin{array}{l}\left| {{y_A} - {y_B}} \right| = 1 \\\Leftrightarrow \left| {\frac{1}{2}g{t^2} - \frac{1}{2}g{{\left( {t + 0,1} \right)}^2}} \right| = 1\\ \Leftrightarrow t = 1,05{\rm{s}}\end{array}\)

Chọn D

Câu 15:

Gọi t là thời gian từ lúc vật bắt đầu rơi đến khi chạm đất, ta có:

\({s_1} = h = \frac{1}{2}g{t^2}\)

Quãng đường vật đi được trong (t-1) s là:

\({s_2} = \frac{1}{2}g{\left( {t - 1} \right)^2}\)

Quãng đường vật đi trong giây cuối cùng là:

\(\begin{array}{l}\Delta s = {s_1} - {s_2} \Leftrightarrow 35 = \frac{1}{2}g{t^2} - \frac{1}{2}g{\left( {t - 1} \right)^2}\\ \Leftrightarrow 10t - 5 = 35 \Leftrightarrow t = 4{\rm{s}}\end{array}\)

Chọn A

Câu 16:

Chọn B

Câu 17:

Chu kì của chất điểm là:

\(T = \frac{t}{n} = \frac{{60}}{{120}} = 0,5{\rm{s}}\)

Chọn A

Câu 18:

Trong chuyển động tròn đều vectơ vận tốc thay đổi về hướng, độ lớn không đổi.

Chọn C

Câu 19:

Gọi vật 1 là thuyền; vật 2 là nước; vật 3 là bờ

Theo đề bài, ta có:

\({v_{13}} = {v_{12}} - {v_{23}} = 6,5 - 1,5 = 5km/h\)

Chọn A

Câu 20:

Đổi \(8km/s = \frac{8}{{1/3600}} = 28800km/h\)

Ta có: \(v = r\omega  \Rightarrow \omega  = \frac{v}{r} = \frac{v}{{h + R}}\)

Chu kì quay của vệ tinh là:

\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{v}{{h + R}}}}\\ = \frac{{2\pi .\left( {h + R} \right)}}{v} = \frac{{2\pi .\left( {600 + 6400} \right)}}{{28800}} = \frac{{35}}{{72}}\pi \left( h \right)\)

\( \approx 1h31ph35{\rm{s}}\)

Chọn C