Đề kiểm tra 45 phút - Đề số 7 - Chương 1 - Hình học 9

Đề bài

Bài 1. Không dùng bảng số và máy tính , hãy tính:

\(A = 3\tan 67^\circ  + 5{\cos ^2}16^\circ  - 3\cot 23^\circ  \)\(\;+ 5{\cos ^2}74^\circ  - {{\cot 37^\circ } \over {\tan 53^\circ }}\)

Bài 2. Cho tam giác ABC vuông tại C có \({\mathop{\rm sinA}\nolimits}  = {3 \over 5}\). Không tính số đo góc A. Hãy tính cosA, tanA, cotA.

Bài 3. Cho tam giác ABC. Chứng minh rằng \({S_{ABC}} = {1 \over 2}AB.AC.\sin A\)

Bài 4. Cho tam giác ABC vuông tại A có \(AB = 9cm, \;BC = 15cm\), đường cao AH.

a. Tính AH và CH.

b. Qua B vẽ đường thẳng vuông góc với BC cắt đường thẳng AC tại D. Tia phân giác của góc C cắt AB tại N và BD tại M. Chứng minh \(CN.CD = CM.CB\)

c. Chứng minh \({{NA} \over {MD}} = {{CA} \over {CD}}\)

(Tính độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ nhất, nếu có).

Lời giải chi tiết

Bài 1. Ta có:

\(\eqalign{   A &= 3\tan 67^\circ  + 5{\cos ^2}16^\circ  - 3\cot 23^\circ  + 5{\cos ^2}74^\circ  - {{\cot 37^\circ } \over {\tan 53^\circ }}  \cr  &  = 3\tan 67^\circ  - 3\cot 23^\circ  + 5{\cos ^2}16^\circ  + 5{\cos ^2}74^\circ  - {{\cot 37^\circ } \over {\tan 53^\circ }}  \cr  &  = 3\tan 67^\circ  - 3\tan 67^\circ  + 5{\cos ^2}16^\circ  + 5{\sin ^2}16 - {{\tan 53^\circ } \over {\tan 53^\circ }}  \cr  &  = 0 + 5\left( {{{\cos }^2}16^\circ  + {{\sin }^2}16^\circ } \right) - 1 = 5 - 1 = 4 \cr} \)

Bài 2.

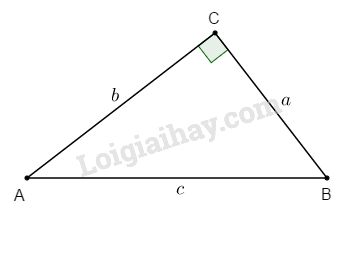
\(\sin A = {3 \over 5}\) hay \({a \over c} = {3 \over 5} \Rightarrow a = {{3c} \over 5} \Rightarrow {a^2} = {{9{c^2}} \over {25}}\)

Theo định lí Pi-ta-go, ta có:

\(\eqalign{  & {b^2} = {c^2} - {a^2} = {c^2} - {{9{c^2}} \over {25}} = {{16{c^2}} \over {25}}  \cr  &  \Rightarrow b = {4 \over 5}c \Rightarrow {b \over c} = {4 \over 5} \cr} \)

Vậy \(\cos A = {4 \over 5},\,tanA = {3 \over 4},\,\cot A = {4 \over 3}\)

Cách khác : Ta có: \({\sin ^2}A + {\cos ^2}A = 1 \)\(\,\Rightarrow {\cos ^2}A = 1 - {\sin ^2}A\)

\(\eqalign{  &  \Rightarrow \cos A = \sqrt {1 - {{\sin }^2}A}  \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {1 - {{\left( {{3 \over 5}} \right)}^2}}  = \sqrt {{{16} \over {25}}}  = {4 \over 5}  \cr  & \tan A = {{\sin A} \over {\cos A}} = {3 \over 5}:{4 \over 5} = {3 \over 4}\cr&\cot A = {4 \over 3} \cr} \)

Bài 3.

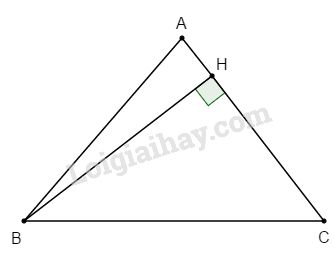
Kẻ đường cao BH của tam giác ABC, ta có:

\(BH = AB.\sin A\)

\( \Rightarrow {S_{ABC}} = {1 \over 2}AC.BH\)\(\; = {1 \over 2}AB.AC.\sin A\)

Bài 4.

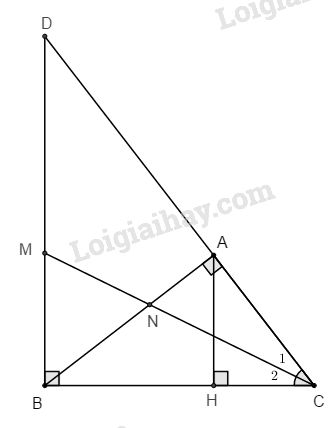
a. Theo định lí Pi-ta-go, ta có:

\(A{C^2} = B{C^2} - A{B^2} = {15^2} - {9^2} = 144\)

\(\Rightarrow AC = 12\,\left( {cm} \right)\)

Tam giác ABC vuông tại A có đường cao AH, ta có:

\(AH.BC = AB.AC\) (hệ thức lượng)

\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{9.12} \over {15}} = 7,2\,\left( {cm} \right)\)

Áp dụng hệ thức lượng trong tam giác vuông, ta có:

\(A{C^2} = BC.CH \)

\(\Rightarrow CH = {{A{C^2}} \over {BC}} = {{{{12}^2}} \over {15}} = 9,6\,\left( {cm} \right)\)

b. Ta có: \({\widehat C_1} = {\widehat C_2}\) (giả thiết)

⇒ ∆CAN đồng dạng ∆CBM (g.g)

\( \Rightarrow {{CN} \over {CM}} = {{CA} \over {CB}}\) (1)

Dẽ thấy ∆CAB đồng dạng ∆CBD (g.g)

\( \Rightarrow {{CA} \over {CB}} = {{CB} \over {CD}}\) (2)

Từ (1) và (2) \( \Rightarrow {{CN} \over {CM}} = {{CB} \over {CD}} \Rightarrow CN.CD = CM.CB\)

c. ∆CAN đồng dạng ∆CBM (chứng minh trên), ta có: \({{NA} \over {CA}} = {{MB} \over {CM}}\) (3)

Tia CM là phân giác của ∆CBD \( \Rightarrow {{MB} \over {MD}} = {{CB} \over {CD}} \Rightarrow {{MB} \over {CB}} = {{MD} \over {CD}}\) (4)

Từ (3) và (4) \( \Rightarrow {{NA} \over {CA}} = {{MD} \over {CD}} \Rightarrow {{NA} \over {MD}} = {{CA} \over {CD}}\)