Đề kiểm tra 15 phút - Đề số 4 - Bài 4 - Chương 1 - Hình học 9

Đề bài

Bài 1. Tính \(A = {{{{\sin }^2}\alpha  - {{\cos }^2}\alpha } \over {\sin \alpha .\cos \alpha }}\) biết \(\tan \alpha  = \sqrt 3 .\)

Bài 2. Cho ∆ABC cân tại A, đường cao \(BK = h\) và \(\widehat {ABC} = \alpha .\) Tính các cạnh của tam giác theo h và \(α\).

Lời giải chi tiết

Bài 1. Chia cả tử và mẫu của biểu thức A cho \({\cos ^2}\alpha ,\) ta có: \(A = {{{{\tan }^2}\alpha  - 1} \over {\tan \alpha }}\)

Thay \(\tan \alpha  = \sqrt 3 ,\) ta có: \(A = {{{{\left( {\sqrt 3 } \right)}^2} - 1} \over {\sqrt 3 }} = {{3 - 1} \over {\sqrt 3 }} = {2 \over {\sqrt 3 }} = {{2\sqrt 3 } \over 3}\)

Bài 2.

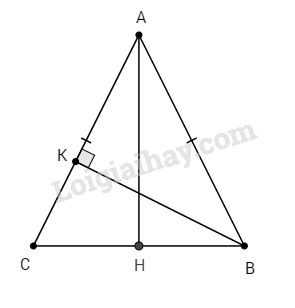
∆ABC cân tại A nên \(\widehat {ACB} = \widehat {ABC} = \alpha \)

Lại có ∆BKC vuông tại K có \(\widehat C = \alpha ,\) ta có:

\(BK = BC.\sin \alpha  \Rightarrow BC = {{BK} \over {\sin \alpha }} = {h \over {\sin \alpha }}\)

Kẻ đường cao AH, ta có: ∆ABC cân tại A nên AH đồng thời là trung tuyến

hay \(BH = CH = {{BC} \over 2} = {h \over {2\sin \alpha }}\)

Xét tam giác vuông AHB có: \(BH = AB.\cos B = AB.\cos α\)

\( \Rightarrow AB = {{BH} \over {\cos \alpha }} \)\(\;= {h \over {2\sin \alpha }}:\cos \alpha  = {h \over {2\sin \alpha \cos \alpha }}\)

Do đó: \(AC = AB = {h \over {2\sin \alpha .\cos \alpha }}\)