Câu hỏi trắc nghiệm ôn tập chương II trang 78 SGK Hình học 11 Nâng cao

LG 1

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm tam giác BCD. Khi ấy, giao điểm của đường thẳng MG và mp(ABC) là :

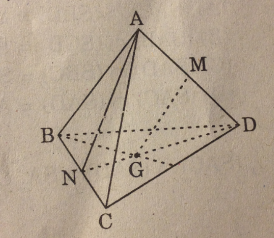
A. Điểm C

B. Giao điểm của đường thẳng MG và đường thẳng AN

C. Điểm N

D. Giao điểm của đường thẳng MG và đường thẳng BC

Giải chi tiết:

NA và MG cùng thuộc mặt phẳng (AND) và không song song nhau nên cắt nhau tại I thì I = MG ∩ (ABC)

Chọn (B)

LG 2

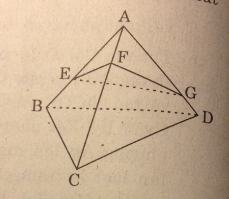
Cho tứ diện ABCD và ba điểm E, F, G lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là :

A. Một đoạn thẳng’

B. Một tam giác

C. Một tứ giác

D. Một ngũ giác

Giải chi tiết:

Thiết diện của tứ diện ABCD khi cắt bởi mp(EFG) là tam giác EFG.

Chọn (B)

LG 3

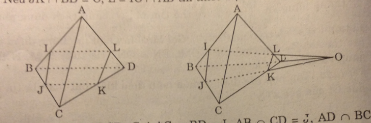
Cho tứ diện ABCD và ba điểm I, J, K lần lượt nằm trên ba cạnh AB, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(IJK) là :

A. Một tam giác

B. Một tứ giác

C. Một hình thang

D. Một ngũ giác

Giải chi tiết:

* Nếu JK // BD thì BD // (IJK) nên (IJK) ∩ (ABD) = IL // BD. Thiết diện là hình thang IJKL.

* Nếu JK ∩ BD = O, L = IO ∩ AD thì thiết diện là tứ giác IJKL.

Chọn (B)

LG 4

Cho hình chóp S.ABCD. Gọi AC ∩ BD = I, AB ∩ CD = J, AD ∩ BC = K. Đẳng thức nào sai trong các đẳng thức sau đây ?

A. (SAD) ∩ (SBD) = SI

B. (SAD) ∩ (SCD) = SJ

C. (SAD) ∩ (SBC) = SK

D. (SAC) ∩ (SAD) = AB

Giải chi tiết:

 (SAC) ∩ (SAD) = SA

Chọn (D)

LG 5

Cho hình chóp S.ABCD. Một mặt phẳng không đi qua đỉnh nào của hình chóp cắt các cạnh SA, SB, SC, SD lần lượt tại A’, B’, C’, D’. Gọi O là giao điểm AC và BD. Tìm mệnh đề đúng trong các mệnh đề sau đây

A. Các đường thẳng A’C’, B’D’, SO đôi một chéo nhau

B. Các đường thẳng A’C, B’D’, SO đồng phẳng

C. Các đường thẳng A’C’, B’D’, SO đồng quy

D. Hai đường thẳng A’C’ và B’D’ cắt nhau còn hai đường thẳng A’C’ và SO chéo nhau

Giải chi tiết:

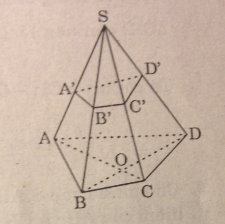
Ta có: A’C’ ⊂ mp(SAC)

B’D’ ⊂ mp(SBD)

Và (SAC) ∩ (SBD) = SO

Gọi I  = A’C’ ∩ B’D’

Thì I ϵ SO do đó A’C’, B’D’, SO đồng quy.

Chọn (C)

LG 6

Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng ?

A. Đường thẳng GE song song với đường thẳng CD

B. Đường thẳng GE cắt đường thẳng CD

C. Hai đường thẳng GE và CD chéo nhau

D. Đường thẳng GE cắt đường thẳng AD

Giải chi tiết:

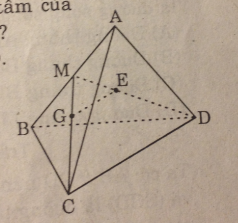
Gọi M là trung điểm AB

Trong ΔMCD ta có : \({{MG} \over {MC}} = {{ME} \over {MD}} = {1 \over 3}\) (tính chất trọng tâm)

\( \Rightarrow GE//CD\)

Chọn (A)

LG 7

Cho tứ diện ABCD. Gọi M, K lần lượt là trung điểm của BC và AC, N là điểm trên cạnh BD sao cho BN = 2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau đây, mệnh đề nào đúng ?

A. AF = FD

B. AF = 2FD

C. AF = 3FD

D. FD = 2AF

Giải chi tiết:

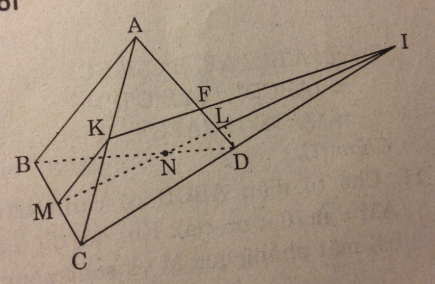
Gọi I = MN ∩ CD

⇒ F = KI ∩ AD = AD ∩ (MNK)

Kẻ DL // BC (L ϵ MI)

\({{DL} \over {BM}} = {{DN} \over {BN}} = {1 \over 2} \Rightarrow DL = {1 \over 2}CM\)

⇒ D là trung điểm CI.

Từ đó suy ra F là trọng tâm ΔACI nên AF = 2FD.

Chọn (B)

LG 8

Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :

A. \({{{a^2}\sqrt 3 } \over 2}\)

B. \({{{a^2}\sqrt 2 } \over 4}\)

C. \({{{a^2}\sqrt 2 } \over 6}\)

D. \({{{a^2}\sqrt 3 } \over 4}\)

Giải chi tiết:

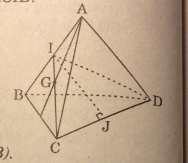
Gọi I là trung điểm của AB. Thiết diện cần tìm là ΔCID

Gọi J là trung điểm CD

ΔCID cân nên IJ ⊥ CD ⇒ \({S_{ICD}} = {1 \over 2}IJ.CD\)

Ta có:

\(\eqalign{  & I{J^2} = C{I^2} - C{J^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {{{a^2}} \over 4} = {{{a^2}} \over 2}  \cr  &  \Rightarrow IJ = {{a\sqrt 2 } \over 2} \Rightarrow {S_{ICD}} = {1 \over 2}.{{a\sqrt 2 } \over 2}.a = {{{a^2}\sqrt 2 } \over 4} \cr} \)

Chọn (B)

LG 9

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. Khi ấy, giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với :

A. Đường thẳng AD

B. Đường thẳng BJ

C. Đường thẳng BI

D. Đường thẳng IJ

Giải chi tiết:

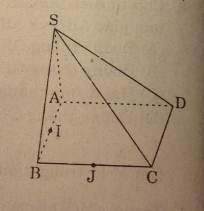
Ta có: AB // CD nên giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song với AB.

Chọn (C)

LG 10

Cho hình chóp S.ABCD có đáy là một hình bình hành. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC và SD. Tìm mệnh đề đúng trong các mệnh đề sau đây :

A. A’B’ // mp(SAD)

B. A’C’ // mp(SBD)

C. mp(A’C’D’) // mp(ABC)

D. A’C’ // BD

Giải chi tiết:

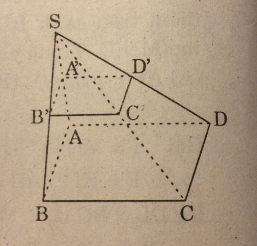
Ta có: A’B’ // AB, B’C’ // BC

⇒ (ABCD) // (A’B’C’D’)

⇒ (A’C’D’) // (ABC)

Chọn (C)

LG 11

Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:

A. \({{{m^2}\sqrt 3 } \over 4}\)

B. \({{{{\left( {a - m} \right)}^2}\sqrt 2 } \over 2}\)

C. \({{{{\left( {a + m} \right)}^2}} \over 4}\)

D. \({{{{\left( {a - m} \right)}^2}\sqrt 3 } \over 4}\)

Giải chi tiết:

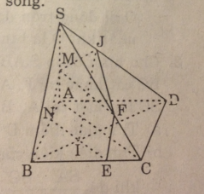
Vẽ MN // AC (N ϵ BC)

MP // AD (P ϵ BD)

Thiết diện cần tìm là ΔMNP

Ta có: \(\Delta MNP\infty \Delta ACD\) tỉ số \({{MP} \over {AD}} = {{BM} \over {AB}} = {{a - m} \over a}\)

\({S_{MNP}} = {\left( {{{a - m} \over a}} \right)^2}.{S_{ABC}} = {\left( {{{a - m} \over a}} \right)^2}.{{{a^2}\sqrt 3 } \over 4} = {\left( {a - m} \right)^2}{{\sqrt 3 } \over 4}\)

Chọn (D)

LG 12

Giải chi tiết:

Cho hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) song song với AC và SB lần lượt cắt các cạnh SA, AB, BC, SC, SD, BD tại M, N, E, F, I, J. Trong các mệnh đề sau đây, mệnh đề nào đúng ?

A. Bốn đường thẳng MN, EF, IJ, SB đôi một song song

B. Bốn đường thẳng MN, EF, IJ, SB đồng quy

C. Bốn đường thẳng MN, EF, IJ, SB đồng phẳng

D. Cả ba mệnh đề trên đều sai.

Giải

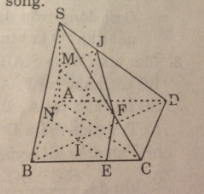
(P) // AC và (P) // SB nên (P) cắt các mp(ASB), (SBC), (SBD) theo các giao tuyến MN // EF // IJ // SB.

Chọn (A)