Câu 6 trang 120 SGK Hình học 11 Nâng cao

Đề bài

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABB’A’ là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB’.

a. Xác định thiết diện của hình lăng trụ đã cho khi cắt bởi (P). Thiết diện là hình gì ?

b. Tính diện tích thiết diện nói trên.

Lời giải chi tiết

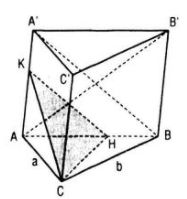
a. Kẻ đường cao CH của tam giác vuông ABC thì CH ⊥ AB’ (định lí ba đường vuông góc).

Trong mp(ABB’A’) kẻ đường thẳng Ht vuông góc với AB’. Khi đó (P) chính là mp(CHt).

Chú ý rằng do ABB’A’ là hình vuông nên AB’ ⊥ A’B. Vậy Ht // A’B, từ đó Ht cắt AA’ tại điểm K thuộc đoạn AA’.

Như vậy, thiết diện của hình lăng trụ ABC.A’B’C’ khi cắt bởi mp(P) là tam giác CHK.

Do CH ⊥ AB, mp(ABB’A’) ⊥ mp(ABC) nên CH ⊥ (ABB’A’), từ đó tam giác CHK vuông tại H.