Câu 3 trang 120 SGK Hình học 11 Nâng cao
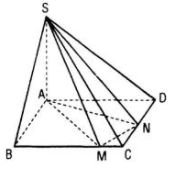
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
a. Hai mặt phẳng (SAM) và (SAN) tạo với nhau góc 45˚ ;
b. Hai mặt phẳng (SAM) và (SMN) vuông góc với nhau.
Lời giải chi tiết
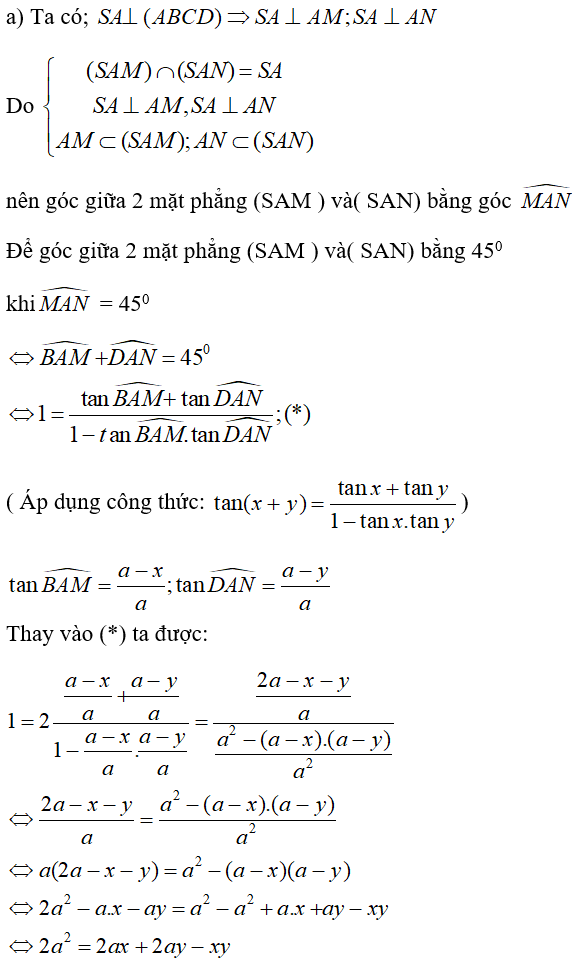
Đó là hệ thức liên hệ giữa x và y để các mặt phẳng (SAM) và (SAN) tạo với nhau góc 45˚
b. Ta có: (SAM) ⊥ (ABCD), từ đó nếu (SMN) ⊥ (SAM) thì giao tuyến MN của (SMN) và (ABCD) sẽ vuông góc với (SAM), tức MN ⊥ AM.
Ngược lại, nếu có MN ⊥ AM thì do SA ⊥ MN nên MN ⊥ (SAM), suy ra (SMN) ⊥ (SAM)
Vậy (SAM) ⊥ (SMN) khi và chỉ khi \(\widehat {AMN} = 90^\circ .\)
\(\eqalign{ & \Leftrightarrow {a^2} + {\left( {a - x} \right)^2} + {x^2} + {y^2} \cr &= {a^2} + {\left( {a - y} \right)^2} \cr & \Leftrightarrow ay = x\left( {a - x} \right)\cr & \text{ với } 0 \le x \le a,0 \le y \le a. \cr} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 3 trang 120 SGK Hình học 11 Nâng cao timdapan.com"







