Câu 33 trang 68 SGK Hình học 11 Nâng cao

Đề bài

Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành

Lời giải chi tiết

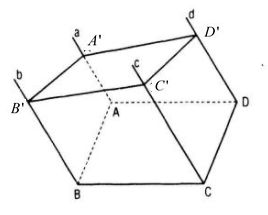
Ta có: \(\left\{ {\matrix{   {a//b}  \cr   {AD//BC } \cr   {a \cap AD=A }  \cr } } \right.\Rightarrow \left( {a,d} \right)//\left( {b,c} \right) \)

Tương tự (a, b) // (c, d).

Vì hai mặt phẳng (a, b) và (c, d) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này

lần lượt theo hai giao tuyến A’B’ và C’D’ song song nhau.

Tương tự A’D’// B’C’.

Vậy A’B’C’D’ là hình bình hành.