Câu 30 trang 55 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M và N lần lượt là trung điểm của CD và AB.
Đề bài
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M và N lần lượt là trung điểm của CD và AB.
a) Hãy xác định điểm \(I \in AC,\,J \in DN\) sao cho IJ//BM.
b) Tính độ dài đoạn thẳng IJ theo a.
Lời giải chi tiết
a) Trong mp(BCD), từ D kẻ đường thẳng song song với BM cắt CB tại K. Đường thẳng KN cắt AC tại I. Trong mp(IKD), từ I kẻ đường thẳng song song với DK cắt đường thẳng DN tại J. Khi đó theo cách dựng ta có IJ // BM.
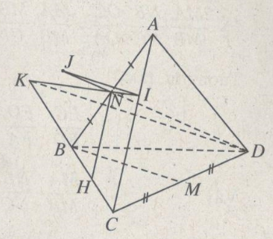
b) Do BM là đường trung bình của tam giác CKD nên
\(KD = 2BM = 2.{{a\sqrt 3 } \over 2} = a\sqrt 3 \)
Gọi H là trung điểm của BC. Khi đó:
\(\eqalign{
& NH//AC \Rightarrow {{NK} \over {NI}} = {{KH} \over {HC}} = {{3HC} \over {HC}} = 3 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow NK = 3NI \Rightarrow KD = 3IJ \cr} \)
Vậy \(IJ = {1 \over 3}KD = {{a\sqrt 3 } \over 3}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 30 trang 55 Sách bài tập Hình học 11 nâng cao. timdapan.com"







