Câu 22 trang 55 SGK Hình học 11 Nâng cao
Gọi G là trọng tâm của tứ diện ABCD a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’
Đề bài
Gọi G là trọng tâm của tứ diện ABCD
a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy
b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’
Lời giải chi tiết
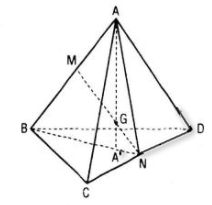
a. Trong mp(ABN) gọi A’ là giao điểm của AG với trung tuyến BN của ΔBCD. Ta chứng minh :
A’B = 2A’N
Áp dụng định lí Menelaus trong ΔBMN với cát tuyến AGA’ ta có :
\({{AM} \over {AB}}.{{GN} \over {GM}}.{{A'B} \over {A'N}} = 1 \Rightarrow {1 \over 2}.1.{{A'B} \over {A'N}} = 1 \Rightarrow A'B = 2A'N\)
Vậy A’ là trọng tâm của ΔBCD
Tương tự BG ,CG, DG lần lượt đi qua trọng tâm B’, C’, D’ của tam giác ACD, ABD, ABC.
b. Chứng minh GA = 3GA’
Áp dụng định lí Menelaus trong ΔABA’ với cát tuyến MGN ta có :
\({{MA} \over {MB}}.{{GA'} \over {GA}}.{{NB} \over {NA'}} = 1 \Rightarrow 1.{{GA'} \over {GA}}.3 = 1 \)
\(\Rightarrow GA = 3GA'\,\,\left( {dpcm} \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 22 trang 55 SGK Hình học 11 Nâng cao timdapan.com"







