Câu 20 trang 55 SGK Hình học 11 Nâng cao

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên ba cạnh AB, CD, BC. Hãy xác định giao điểm S của mp(PQR) với cạnh AD nếu:

LG a

PR // AC

Giải chi tiết:

 Trường hợp PR // AC

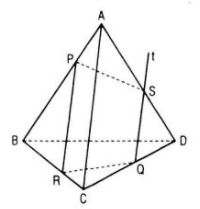
Hai mặt phẳng (PQR) và (ACD) có điểm chung Q và lần lượt chứa hai đường thẳng song song PR và AC nên :

(PQR) ∩ (ACD) = Qt // AC

Gọi {S} = Qt ∩ AD thì {S} = AD ∩ (PQR)

LG b

 PR cắt AC

Giải chi tiết:

Trường hợp PR cắt AC

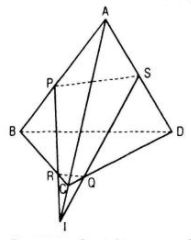
Giả sử {I} = PR ∩ AC

⇒ (PQR) ∩ (ACD) = QI

Trong mp(ACD) ta có

{S} = QI ∩ AD thì {S} = AD ∩ (PQR)