Bài tập 2 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình thang ABCD (AB, CD là hai đáy). Gọi M, N, P, Q lần lượt là trung điểmcủa AB, AC, CD, BD.
Đề bài
Cho hình thang ABCD (AB, CD là hai đáy). Gọi M, N, P, Q lần lượt là trung điểmcủa AB, AC, CD, BD.
a) Chứng minh rằng tứ giác MNPQ là hình bình hành.
b) Hình thang ABCD cần có thêm điều kiện gì để tứ giác MNPQ laanf lượt trở thành :
- Hình thoi
- Hình chữ nhật
- Hình vuông
Lời giải chi tiết
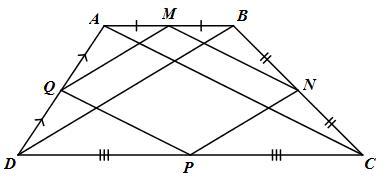
a) M, N lần lượt là trung điểm của AB và BC (gt);
\( \Rightarrow MN\) là đường trung bình của tam giác ABC
\( \Rightarrow MN//AC\) và ..
Q, P lần lượt là trung điểm của AD và CD (gt);
\( \Rightarrow QP\) là đường trung bình của tam giác ADC
\( \Rightarrow QP//AC\) và \(QP = {1 \over 2}AC\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MN//QP\) và \(MN = QP\)
Vậy tư giác MNPQ là hình bình hành.
b) Ta có tứ giác MNPQ là hình bình hành.
MN // AC, \(MN = {{AC} \over 2}\) (MN là đường trung bình của tam giác ABC)
MQ // BD, \(MQ = {{BD} \over 2}\) (MQ là đường trung bình của tam giác ABD)
* Tứ giác MNPQ là hình thoi \( \Leftrightarrow \) Hình bình hành MNPQ có \(MN = MQ \Leftrightarrow AC = BD\)
Vậy hình thanh ABCD cần có thêm điều kiện \(AC = BD\) để tứ giác MNPQ là hình thoi.
* Tứ giác MNPQ là hình chữ nhật \( \Leftrightarrow \) Hình bình hành MNPQ có \(\widehat {NMQ} = {90^0}\)
\( \Rightarrow MN \bot MQ \Leftrightarrow MQ \bot AC \Leftrightarrow AC \bot BD\)
Vậy hình thang ABCD cần có thêm điều kiện \(AC \bot BD\) để tứ giác MNPQ là hình chữ nhật.
* Tứ giác MNPQ là hình vuông \( \Leftrightarrow \) Hình thoi MNPQ có \(\widehat {NMQ} = {90^0} \Leftrightarrow AC = BD\) và \(AC \bot BD\)
Vậy hình thang ABCD cần thêm điều kiện \(AC = BD,\,\,AC \bot BD\) để tứ giác MNPQ là hình vuông.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 2 trang 140 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"