Bài 8 trang 15 SGK Hình học 12 Nâng cao

Cho hình lập phương \(ABCD.A'B'C'D'\). Chứng minh rằng :

LG a

Các hình chóp \(A.A'B'C'D'\) và \(C.ABCD\) bằng nhau ;

Giải chi tiết:

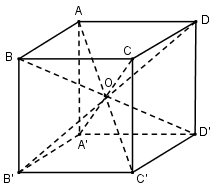
Gọi \(O\) là tâm của hình lập phương.

Phép đối xứng tâm \(O\) biến các đỉnh của hình chóp \(A.A’B’C’D’\) thành các đỉnh của hình chóp \(C’.ABCD\).

Vậy hai hình chóp đó bằng nhau.

LG b

Các hình lăng trụ \(ABC.A'B'C'\) và \(AA'D'.BB'C'\) bằng nhau.

Giải chi tiết:

Phép đối xứng qua mp\((ADC’B’)\) biến các đỉnh của hình lăng trụ \(ABC.A’B’C’\) thành các đỉnh của lăng trụ \(AA’D’.BB’C’\) nên hai hình lăng trụ đó bằng nhau.