Bài 8 trang 128 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn (O) và hai dây AB và CD
Đề bài
Cho đường tròn (O) và hai dây AB và CD sao cho AB < CD. Hai đường thẳng AB và CD cắt nhau tại điểm K nằm ngoài đường tròn. Đường tròn tâm O, bán kính OK cắt hai tia KA và KC lần lượt tại M và N. Chứng minh KM < KN.
Phương pháp giải - Xem chi tiết
Sử dụng định lí : Trong cùng một đường tròn, dây lớn hơn thì gần tâm hơn.
Lời giải chi tiết
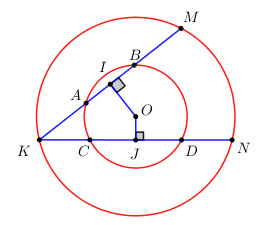
Kẻ \(KI \bot AB,\,\,KJ \bot CD\)\(\,\,\left( {I \in AB,\,\,J \in CD} \right)\) ta có :
\(AB < CD \Rightarrow OI > OJ\)(trong một đường tròn, dây ngắn hơn thì xa tâm hơn).
Xét \(\left( {O;OK} \right)\) có \(OI \bot KM,\,\,OJ \bot KN\), lại có \(OI > OJ\,\,\left( {cmt} \right) \Rightarrow KM < KN\) (trong một đường tròn, dây nào xa tâm hơn thì ngắn hơn).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 8 trang 128 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 8 trang 128 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







