Bài 1 trang 128 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn (O) và điểm M nằm bên trong đường tròn.
Đề bài
Cho đường tròn (O) và điểm M nằm bên trong đường tròn. AB là dây qua M vuông góc với OM ; CD là dây qua M không vuông góc với OM. Chứng minh rằng AB < CD. ( Hướng dẫn : Kẻ OI vuông góc CD, OI < OM ).
Phương pháp giải - Xem chi tiết
Kẻ \(OI \bot CD\), chứng minh \(OI < OM\). Sử dụng định lí: Trong một đường tròn, dây gần tâm hơn thì lớn hơn.
Lời giải chi tiết
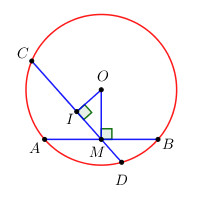
Kẻ \(OI \bot CD,\,\,M \in CD \Rightarrow OI \bot IM\).
Xét tam giác vuông OMI có: \(OI < OM\) (trong tam giác vuông, cạnh góc vuông nhỏ hơn cạnh huyền).
Mà \(OI \bot CD,\,\,OM \bot AB\) nên \(CD > AB\) (trong một đường tròn, dây gần tâm hơn thì lớn hơn).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 128 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 128 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







