Bài 7 trang 128 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn tâm O, hai dây CD và EF bằng nhau
Đề bài
Cho đường tròn tâm O, hai dây CD và EF bằng nhau và vuông góc với nhau tại I. Biết IC = 2 cm, ID = 4 cm. Tính khoảng cách từ O đến dây EF.
Phương pháp giải - Xem chi tiết
+) Kẻ \(OH \bot EF,\,\,OK \bot CD\). Chứng minh tứ giác OHIK là hình vuông.
+) Chứng minh K là trung điểm của CD. Cộng trừ đoạn thẳng, tính KI.
Lời giải chi tiết
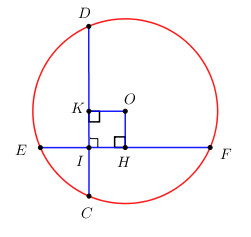
Kẻ \(OH \bot EF,\,\,OK \bot CD\).
Xét tứ giác OHIK có : \(\widehat {OHI} = \widehat {OKI} = \widehat {HIK} = {90^0} \Rightarrow \) Tứ giác \(OHIK\) là hình chữ nhật (tứ giác có 3 góc vuông).
Lại có \(EF = CD \Rightarrow OH = OK\) (trong một đường tròn, hai dây bằng nhau thì cách đều tâm)
\( \Rightarrow OHIK\) là hình vuông (Hình chữ nhật có 2 cạnh kề bằng nhau) \( \Rightarrow OH = KI\).
Ta có \(CD = IC + ID = 2 + 4 = 6\,\,\left( {cm} \right)\).
\(OK \bot CD \Rightarrow K\) là trung điểm của CD \( \Rightarrow KC = KD = \dfrac{1}{2}CD = 3\,\,\left( {cm} \right)\).
Vậy \(KI = KC - IC = 3 - 2 = 1\,\,\left( {cm} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 128 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







