Bài 7 trang 171 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua E vuông góc BE = BA. Đường thẳng qua E vuông góc với BC cắt AC ở F và cắt AB ở G.
Đề bài
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua E vuông góc BE = BA. Đường thẳng qua E vuông góc với BC cắt AC ở F và cắt AB ở G.
a) Chứng minh rằng tam giác AEF cân.
b) Chứng minh rằng AC = GE.
c) Kẻ \(AH \bot BC(H \in BC).\) Gọi I là giao điểm của AH và BF. Chứng minh rằng tam giác AIF cân.
Lời giải chi tiết
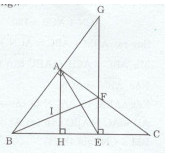
a)Xét tam giác ABF vuông tại A và tam giác EBF vuông tại E có:
BF là cạnh chung.
BA = BE (gt)
Do đó \(\Delta ABF = \Delta EBF\) (cạnh huyền - cạnh góc vuông)
=>AF = EF => tam giác AEF cân tại F.
b) Xét tam giác ABC và EBG có:
\(\widehat {BAC} = \widehat {BEG}( = {90^0})\)
BA = BE (gt)
\(\widehat {ABC}\) là góc chung.
Do đó: \(\Delta ABC = \Delta EBG(g.c.g) \Rightarrow AC = GE.\)
c) Ta có: \(\eqalign{ & AH \bot BC(gt) \cr & EF \bot BC(gt) \cr} \)
\(\Rightarrow AH = EF \Rightarrow \widehat {AIF} = \widehat {BFE}\) (so le trong)
Mà \(\widehat {AFI} = \widehat {BFE}(\Delta ABF = \Delta EBF) \Rightarrow \widehat {AIF} = \widehat {AFI}.\)
Do đó: tam giác AIF cân tại A.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 171 Tài liệu dạy – học Toán 7 tập 1 timdapan.com"