Bài 2 trang 171 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm.

a) Tính độ dài BC.

b) Gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD. Chứng minh rằng \(\Delta AMB = \Delta DMC.\)

c) Chứng minh rằng tam giác ACD vuông.

Lời giải chi tiết

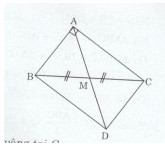
a)Tam giác ABC vuông tại A (gt) \(\Rightarrow B{C^2} = A{B^2} + A{C^2}\)   (định lý Pythapore)

Do đó: \(B{C^2} = {9^2} + {12^2} = 81 + 144 = 225.\)

Mà BC > 0 nên \(BC = \sqrt {225}  = 15(cm).\)

b) Xét tam giác AMB và DMC ta có:

AM = DM (giả thiết)

BM = CM (M là trung điểm của BC)

\(\widehat {AMB} = \widehat {CMD}\)   (hai góc đối đỉnh)

Do đó: \(\Delta AMB = \Delta DMC(c.g.c)\)

c) Ta có: \(\widehat {MBA} = \widehat {MCD}(\Delta AMB = \Delta DMC)\)

Mà hai góc MBA và MCD so le trong. Do đó: AB // CD.

Mà \(AB \bot AC(gt) \Rightarrow AC \bot CD.\)   Vậy tam giác ACD vuông tại C.