Bài 61 trang 13 SBT Hình học 12 Nâng cao

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và cạnh bên SA vuông góc với đáy. Một mặt phẳng \(\left( \alpha  \right)\) đi qua A, vuông góc với cạnh SC cắt SB, SC, SD lần lượt tại B’, C’,D’.

LG 1

Chứng minh rằng tứ giác AB’C’D’ có hai góc đối diện là góc vuông.

Lời giải chi tiết:

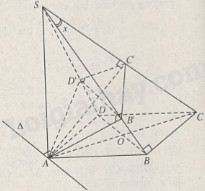
\(SC \bot (AB'C'D') \Rightarrow SC \bot AB'.\) Dễ thấy \(BC \bot (SAB) \Rightarrow BC \bot AB'.\)

Từ đó suy ra :

\(AB' \bot (SBC) \Rightarrow AB' \bot B'C'.\)

Tương tự ta có \(AD' \bot D'C'.\)

Như vậy tứ giác AB’C’D’ có hai góc B’ và D’ vuông.

LG 2

Chứng minh rằng nếu S di chuyển trên đường thẳng vuông góc với mặt phẳng (ABCD) tại A thì \(mp\left( {AB'C'D'} \right)\) luôn đi qua một đường thẳng cố định và các điểm A, B, B’, C, C’, D, D’ cùng cách đều một điểm cố định một khoảng không đổi.

Lời giải chi tiết:

Gọi \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( \alpha  \right)\) và mp(ABCD) .

Do \(\Delta \) thuộc \(\left( \alpha  \right)\)  nên \(\Delta  \bot SC\).

Theo định lý ba đường vuông góc, ta có \(\Delta  \bot AC\). Hơn nữa, \(\Delta \) nằm trong mp(ABCD) và đi qua điểm A có định, vậy \(\Delta \) là đường thẳng cố định.

Do \(AB' \bot (SBC),AD' \bot (SCD) \)

\(\Rightarrow AB' \bot B'C,AD' \bot D'C.\)

Các tam giác vuông ABC, ADC, AB’C, AD’C, AC’C có chung cạnh huyền cố định AC, suy ra các đỉnh A, B, C, D, B’, C’, D’ đều cách trung điểm O của AC một khoảng không đổi \({{AC} \over 2}.\)

LG 3

Giả sử góc giữa cạnh SC và mặt bên (SAB) bằng x.

Tính tỉ số giữa thể tích của hình chóp S.AB’C’D’ và thể tích của hình chóp S.ABCD theo x, biết rằng AB = BC.

Lời giải chi tiết:

Cách 1. Do \(BC \bot (SAB)\) nên SB là hình chiếu của SC trên mp(SAB) và do đó \(\widehat {BSC} = x  \). Ta có

\(\eqalign{  & V = {V_{S.ABCD}} = {1 \over 3}{a^2}SA(a = AB = BC),  \cr  & V' = {V_{S.AB'C'D'}} = {1 \over 3}{S_{AB'C'D'}}.SC'. \cr} \)

Do ABCD là hình vuông nên dễ dàng suy ra được SB’=SD’\( \Rightarrow B'D'// BD.\)

Từ đó dễ thấy \(B'D' \bot (SAC) \Rightarrow B'D' \bot AC'\)

\(\Rightarrow {S_{AB'C'D'}} = {1 \over 2}AC'.B'D'.\)

Ta có :

\(SB = BC\cot x = a\cot x,SC = {{BC} \over {{\mathop{\rm sinx}\nolimits} }} = {a \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}}\)

\(\eqalign{  & SA = \sqrt {S{B^2} - A{B^2}}  = {{a\sqrt {\cos 2x} } \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}},\cr&SB' = {{S{A^2}} \over {SB}} = {{a\cos 2x} \over {{\mathop{\rm s}\nolimits} {\rm{inxcosx}}}},  \cr  & SC' = {{S{A^2}} \over {SC}} = {{a\cos 2x} \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}},\cr&B'D' = BD.{{SB'} \over {SB}} = {{a\sqrt 2 \cos 2x} \over {{{\cos }^2}x}},  \cr  & AC' = {{SA.AC} \over {SC}} = a\sqrt {2\cos 2x} . \cr} \)

Vậy \(V = {{{a^3}\sqrt {\cos 2x} } \over {3\sin x}},V' = {{{a^3}{{\cos }^2}2x\sqrt {\cos 2x} } \over {3\sin x{{\cos }^2}x}} \Rightarrow {{V'} \over V} = {{{{\cos }^2}2x} \over {{{\cos }^2}x}}.\)

Cách 2. Dễ thấy :\({{V'} \over V} = {{2{V_{S.AB'C'}}} \over {2{V_{S.ABC}}}} = {{SB'.SC'} \over {SB.SC}}.\)

Từ đó dễ dàng suy ra kết quả cần tìm.