Bài 6 trang 51 SGK Hình học 10 nâng cao

Cho tam giác \(ABC\) vuông ở \(A\) và \(\widehat B = {30^0}\). Tính giá trị của các biểu thức sau

LG a

\(\cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2}\)

Giải chi tiết:

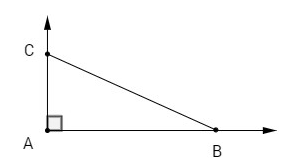
Ta có

 \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {150^0}\,\,;\,\,\,(\overrightarrow {BA} ,\,\overrightarrow {BC} ) = {30^0}\,\,;\,\,\,(\overrightarrow {AC} ,\,\overrightarrow {CB} ) = {120^0}\)

Do đó

\(\eqalign{
& \cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2} = \cos {150^0} + {\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0} + \tan {60^0} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{{ - \sqrt 3 } \over 2} + {1 \over 2} + \sqrt 3 = {{\sqrt 3 + 1} \over 2} \cr} \)

LG b

\(\sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} )\)

Giải chi tiết:

Ta có \((\overrightarrow {CA} ,\,\overrightarrow {BA} ) = {90^0}\), do đó

\(\eqalign{
& \sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} ) = \sin {90^0} + \cos {30^0} + \cos {90^0} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1 + {{\sqrt 3 } \over 2} + 0 = {{2 + \sqrt 3 } \over 2} \cr} \)