Bài 39 trang 79 SGK Toán 8 tập 2

Đề bài

Cho hình thang \(ABCD (AB//CD)\). Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).

a) Chứng minh rằng \(OA.OD = OB.OC\). 

b) Đường thẳng qua \(O\) vuông góc với \(AB\) và \(CD\) theo thứ tự tại \(H\) và \(K\).

Chứng minh rằng \(\dfrac{OH}{OK} = \dfrac{AB}{CD}\)

Lời giải chi tiết

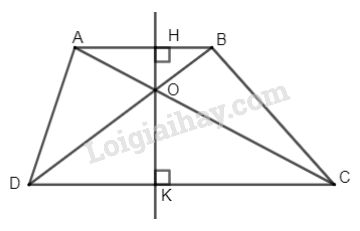
a) Vì \(AB // CD\) (giả thiết)

Áp dụng định lí:Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

\( \Rightarrow ∆AOB ∽ ∆COD\) 

\( \Rightarrow \dfrac{OA}{OC} = \dfrac{OB}{OD}\) (tính chất hai tam giác đồng dạng)

\( \Rightarrow  OA.OD = OC.OB\)

b) Theo câu a) ta có \( ∆AOB ∽ ∆COD\) nên \(\dfrac{OA}{OC} = \dfrac{AB}{CD}\)  (1)

Xét \(∆AOH\) và \(∆COK\) có:

\(\widehat{AHO} = \widehat{CKO} = {90^o}\)

\(\widehat {HOA} = \widehat {K{\rm{O}}C}\) (đối đỉnh)

\( \Rightarrow ∆AOH ∽ ∆COK\) (g-g)

\( \Rightarrow \dfrac{OH}{OK}= \dfrac{OA}{OC}\)  (2) (tính chất hai tam giác đồng dạng)

Từ (1) và (2) \( \Rightarrow \dfrac{OH}{OK} = \dfrac{AB}{CD}\)