Bài 33 trang 125 SGK Toán 9 tập 2

Đề bài

Dụng cụ thể thao

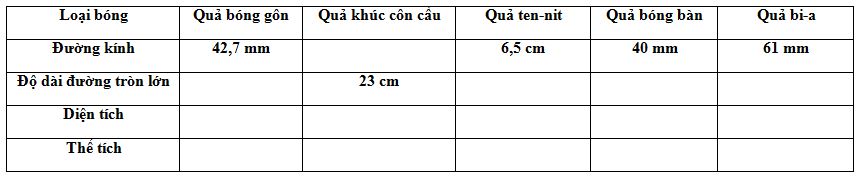
Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai):

Lời giải chi tiết

Dòng thứ nhất: Từ \(\displaystyle C = \pi .d \Rightarrow d = {C \over \pi } = {\rm{ }}{{23} \over {{{22} \over 7}}} = 7,32\) 

Dòng thứ hai: Áp dụng công thức  \(C = π.d\), thay số vào ta được

\(\displaystyle d = 42,7mm \Rightarrow C = {{22} \over 7}.42,7 = 134,08mm\)

\(\displaystyle d = 6,6cm \Rightarrow C = {\rm{ }}{{22} \over 7}.6,6 = 20,41cm\)

\(\displaystyle d = 40mm \Rightarrow C = {\rm{ }}{{22} \over 7}.40 = 125,6mm\)

\(\displaystyle d = 61mm \Rightarrow C = {{22} \over 7}.61 = 191,71mm\)

Dòng thứ ba: ÁP dụng công thức \(S{\rm{ }}  = {\rm{ }}\pi {d^2}\), thay số vào ta được: 

\(\displaystyle d = 42,7mm \Rightarrow S = {{22} \over 7}.42,{7^2} \approx 5730,34(m{m^2})\)

\({\rm{ }} \approx 57,25(c{m^2})\)

\(\displaystyle d = 6,5cm \Rightarrow S = {{22} \over 7}.6,{5^2} = 132,65(c{m^2})\)

\(\displaystyle d = 40mm \Rightarrow S = {{22} \over 7}{.40^2} = 5024(m{m^2})\)

\(\displaystyle d = 61mm \Rightarrow S = {{22} \over 7}.612 = 11683,94(m{m^2})\)

Dòng thứ 4:    

\(d=42,7 mm \Rightarrow V =\dfrac{1}{6} \pi d^3  =\dfrac{1}{6} .3,14. 42,7^3 \\ \approx 40743,85 mm^3 \approx 40,74 cm^3.  \)

\(d=7,32 cm \Rightarrow V =\dfrac{1}{6} \pi d^3  =\dfrac{1}{6} .3,14. 7,32^3 \approx 205,26 cm^3.  \)

\(d=6,5 cm \Rightarrow V =\dfrac{1}{6} \pi d^3  =\dfrac{1}{6} .3,14. 6,5^3 \approx 143,72 cm^3.  \)

\(d=40mm=4 cm \Rightarrow V =\dfrac{1}{6} \pi d^3  =\dfrac{1}{6} .3,14. 4^3 \approx 33,49 cm^3.  \)

\(d=61mm=6,1 cm \Rightarrow V =\dfrac{1}{6} \pi d^3  =\dfrac{1}{6} .3,14. 6,1^3 \approx 118,79 cm^3.  \)

Ta được bảng sau: