Bài 32 trang 128 SGK Toán 8 tập 1
Giải bài 32 trang 128 SGK Toán 8 tập 1. a) Hãy vẽ một tứ giác có độ dài hai đường chéo là 3,6cm, 6cm và hai đường chéo đó vuông góc với nhau.
Đề bài
a) Hãy vẽ một tứ giác có độ dài hai đường chéo là \(3,6cm; 6cm\) và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ?
b) Hãy tính diện tích hình vuông có độ dài đường chéo là \(d\).
Phương pháp giải - Xem chi tiết
Áp dụng cách tính diện tích của một tứ giác có hai đường chéo vuông góc:
- Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.
\({S_{ABCD}}=\dfrac{1}{2} AC. BD\)
Lời giải chi tiết
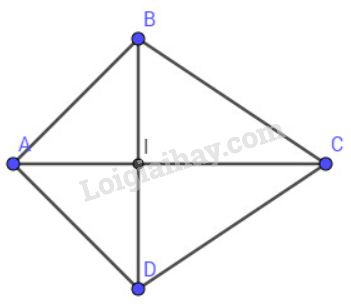
a) Học sinh tự vẽ tứ giác thỏa mãn điều kiện đề bài, chẳng hạn như tứ giác \(ABCD\) ở hình vẽ có:
\(AC = 6cm\)
\(BD = 3,6cm\)
\(AC \perp BD\)
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài:
\(AC = 6cm\)
\(BD = 3,6cm\)
\(AC \perp BD\) tại \(I\) với \(I\) là điểm tùy ý thuộc đoạn \(AC\) và \(BD\)
Diện tích của tứ giác vừa vẽ là:
\(S_{ABCD}= \dfrac{1}{2} AC. BD = \dfrac{1}{2}6. 3,6 = 10,8\) (\(cm^2\))
b) Diện tích hình vuông có độ dài đường chéo là \(d\)
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:
\(S = \dfrac{1}{2} d.d = \dfrac{1}{2} d^2\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 32 trang 128 SGK Toán 8 tập 1 timdapan.com"







