Bài 30 trang 206 SGK giải tích 12 nâng cao

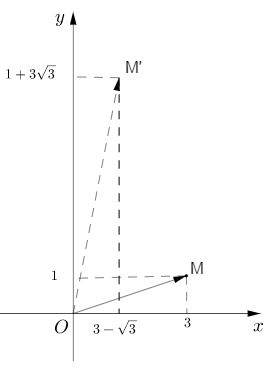
Gọi M, M’ là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số \(z = 3 + i;\,z' = \left( {3 - \sqrt 3 } \right) + \left( {1 + 3\sqrt 3 } \right)i.\)

LG a

Tính \({{z'} \over z};\)

Giải chi tiết:

\(a)\,{{z'} \over z} = {{\left[ {3 - \sqrt 3  + \left( {1 + 3\sqrt 3 } \right)i} \right]\left( {3 - i} \right)} \over {10}} = 1 + \sqrt 3 i\)

LG b

Chứng minh rằng hiệu số acgumen của z’ với acgumen của z là một số đo của góc lượng giác \(\left( {OM,OM'} \right)\). Tính số đo đó.

Giải chi tiết:

Xét tia Ox thì ta có: \(sđ\left( {OM,OM'} \right) = sđ\left( {Ox,OM'} \right) - sđ\left( {Ox,OM} \right)\)

                             \( = \varphi ' - \varphi  = acgumen{{z'} \over z}\) (sai khác \(k2\pi \))

(trong đó \(\varphi \) và \(\varphi '\) theo thứ tự là acgumen của z và z’).

Từ đó do \({{z'} \over z} = 1 + \sqrt 3 i\) có acgumen là \({\pi  \over 3} + k2\pi \,\,\left( {k \in Z} \right)\), nên góc lượng giác \(\left( {OM,OM'} \right)\) có số đo \({\pi  \over 3} + k2\pi \,\,\left( {k \in\mathbb Z} \right)\)