Bài 3 trang 7 SGK Hình học 10

Đề bài

Cho tứ giác \(ABCD\). Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow{AB}\) = \(\overrightarrow{DC}\).

Lời giải chi tiết

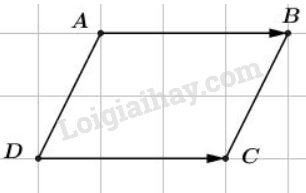
Ta chứng minh hai mệnh đề:

*) Khi \(\overrightarrow{AB}= \overrightarrow{DC}\) thì \(ABCD\) là hình bình hành.

Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:

\(\overrightarrow{AB} = \overrightarrow{DC}  ⇔ \left | \overrightarrow{AB} \right |= \left | \overrightarrow{DC} \right |\) và \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng hướng.

 \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng hướng suy ra \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng phương, suy ra giá của chúng song song với nhau,

hay \(AB // DC\)                          (1)

Ta lại có  \(\left | \overrightarrow{AB} \right |= \left | \overrightarrow{DC} \right |\) suy ra \(AB = DC\)   (2)

Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác \(ABCD\) có một cặp cạnh song song và bằng nhau nên nó là hình bình hành. 

*) Khi \(ABCD\) là hình bình hành thì \(\overrightarrow{AB} = \overrightarrow{DC}\)

  Khi \(ABCD\) là hình bình hành thì \(AB // CD.\) Dễ thấy, từ đây ta suy ra hai vec tơ \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\) cùng hướng     (3)

Mặt khác \(AB = DC\) suy ra \(\left | \overrightarrow{AB} \right |\) = \(\left | \overrightarrow{DC} \right |\)          (4)

Từ (3) và (4) suy ra  \(\overrightarrow{AB}= \overrightarrow{DC}.\)

Như vậy tứ giác \(ABCD\) là hình bình hành khi và chỉ khi  \(\overrightarrow{AB}= \overrightarrow{DC}.\)