Bài 28 Trang 167 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi:
Tính diện tích hình phẳng giới hạn bởi:
LG a
Đồ thị các hàm số \(y = {x^2} - 4\), \(y = - {x^2} - 2x\) và đường thẳng \(x = - 3,x = - 2;\)
Giải chi tiết:
Ta có
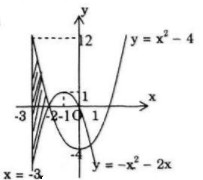
\(S = \int\limits_{ - 3}^{ - 2} {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|} dx = \int\limits_{ - 3}^{ - 2} {\left( {2{x^2} + 2x - 4} \right)} dx\)
\( = 2\int\limits_{ - 3}^{ - 2} {\left( {{x^2} + x - 2} \right)} dx\) vì \(({x^2} + x - 2 \ge 0 \Leftrightarrow x \le - 2\) hoặc \(x \ge 1)\)
\( = 2\left. {\left( {{{{x^3}} \over 3} + {{{x^2}} \over 2} - 2x} \right)} \right|_{ - 3}^{ - 2} = {{11} \over 3}\)
LG b
Đồ thị hai hàm số \(y = {x^2}\) và \(y = - {x^2} - 2x\)
Giải chi tiết:
Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^2} - 4 = - {x^2} - 2x \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 1 \hfill \cr} \right.\)
Do đó \(S = \int\limits_{ - 2}^1 {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|} dx = \int\limits_{ - 2}^1 {\left| {2{x^2} + 2x - 4} \right|} dx\)
\( = - \int\limits_{ - 2}^1 {\left( {2{x^2} + 2x - 4} \right)} dx\) ( vì \( - 2 \le x \le 1 \Leftrightarrow 2{x^2} + 2x - 4 \le 0\))
\( = \int\limits_{ - 2}^1 {\left( { - 2{x^2} - 2x + 4} \right)} dx = \left. {\left( { - {{2{x^3}} \over 3} - {x^2} + 4x} \right)} \right|_{ - 2}^1 = 9\)
LG c
Đồ thị hàm số \(y = {x^3} - 4x\), trục hoành, đường thẳng x=-2 và đường thẳng x=4
Giải chi tiết:
\(S = \int\limits_{ - 2}^4 {\left| {{x^3} - 4x} \right|} dx = \int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)} dx - \int\limits_0^2 {\left( {{x^3} - 4x} \right)} dx + \int\limits_2^4 {\left( {{x^3} - 4x} \right)} dx = 44\)
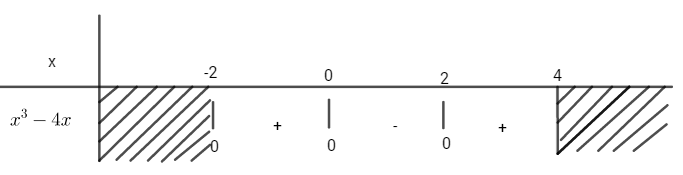
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 28 Trang 167 SGK Đại số và Giải tích 12 Nâng cao timdapan.com"







