Bài 26 trang 23 SGK Đại số và Giải tích 12 Nâng cao

Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là

\(f\left( t \right) = 45{t^2} - {t^3},t = 0,1,2,...,25\)

Nếu coi \(f\) là hàm số xác định trên đoạn \(\left[ {0;25} \right]\) thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\).

LG a

Tính tốc độ truyền bệnh vào ngày thứ \(5\);

Giải chi tiết:

Số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 45{t^2} - {t^3}\), \(t\) nguyên và thuộc \(\left[ {0;25} \right]\)

Để xét tốc độ truyền bệnh người ta xem hàm số \(f\) xác định trên đoạn \(\left[ {0;25} \right]\).

\(f'\left( t \right) = 90t - 3{t^2} = 3t\left( {30 - t} \right)\)

Tốc độ truyền bệnh vào ngày thứ năm là \(f'(5) = 375\) (người/ngày)

LG b

Xác định ngày mà tốc độ truyền bệnh là lớn nhất và tính tốc độ đó;

Giải chi tiết:

\(f''\left( t \right) = 90 - 6t;f''\left( t \right) = 0 \Leftrightarrow t = 15,f'\left( t \right) = 675\)

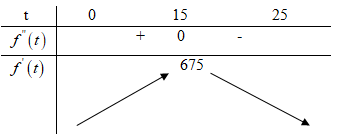
Tốc độ truyền bệnh là lớn nhất vào ngày \(15\).

Tốc độ đó là \(f'\left( {15} \right) = 675\) (người/ngày)

LG c

Xác định các ngày mà tốc độ truyền bệnh lớn hơn \(600\);

Giải chi tiết:

\(f'\left( t \right) > 0 \Leftrightarrow 90t - 3{t^2} > 600 \Leftrightarrow {t^2} - 30t + 200 < 0 \Leftrightarrow 10 < t < 20\)

Từ ngày thứ \(11\) đến ngày thứ \(19\), tốc độ truyền bệnh là lớn hơn \(600\) người mỗi ngày.

LG d

Xét chiều biến thiên của hàm số \(f\) trên đoạn \(\left[ {0;25} \right]\).

Giải chi tiết:

HS tự xét.