Bài 2 trang 126 SGK Hình học 10 nâng cao

Đề bài

Cho tam giác  vuông tại A, AB = c, AC = b . Gọi M là điểm trên cạnh BC sao cho CM = 2BM, N là điểm trên cạnh AB sao cho BN = 2AN (h.106).

a) Biểu thị các vectơ  theo hai vectơ \(\overrightarrow {AM} ,\,\overrightarrow {CN} \) và \(\overrightarrow {AB} ;\,\overrightarrow {AC} \) .

b) Tìm hệ thức liên hệ giữa b và c sao cho \(AM \bot CN\).

Lời giải chi tiết

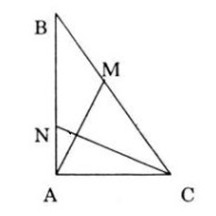
a) Ta có:

\(\overrightarrow {CM}  = 2\overrightarrow {MB} \) \(\Rightarrow \,\,\overrightarrow {AM}  - \overrightarrow {AC}  = 2(\overrightarrow {AB}  - \overrightarrow {AM} )\)

\(\Rightarrow \,\,\overrightarrow {AM}  = {2 \over 3}\overrightarrow {AB}  + {1 \over 3}\overrightarrow {AC} \)

Mặt khác \(\overrightarrow {BN}  = 2\overrightarrow {NA} \) \( \Rightarrow \,\,\overrightarrow {AN}  - \overrightarrow {AB}  =  - 2\overrightarrow {AN} \)\( \Rightarrow 3\overrightarrow {AN}  = \overrightarrow {AB} \)

\(\Rightarrow \,\,\overrightarrow {AN}  = {1 \over 3}\overrightarrow {AB} \)

\( \Rightarrow \,\,\overrightarrow {CN}  = \overrightarrow {AN}  - \overrightarrow {AC}  = {1 \over 3}\overrightarrow {AB}  - \overrightarrow {AC} \)

Cách khác:

\(\begin{array}{l}
\overrightarrow {CM} = 2\overrightarrow {MB} = 2\left( {\overrightarrow {CB} - \overrightarrow {CM} } \right)\\
= 2\overrightarrow {CB} - 2\overrightarrow {CM} \\
\Rightarrow 3\overrightarrow {CM} = 2\overrightarrow {CB} \\
\Rightarrow \overrightarrow {CM} = \frac{2}{3}\overrightarrow {CB} \\
\Rightarrow \overrightarrow {AM} = \overrightarrow {AC} + \overrightarrow {CM} \\
= \overrightarrow {AC} + \frac{2}{3}\overrightarrow {CB} \\
= \overrightarrow {AC} + \frac{2}{3}\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\\
= \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC}
\end{array}\)

b) Ta có 

\(\eqalign{
& \overrightarrow {AM} \bot \overrightarrow {CN} \Leftrightarrow \,\,\overrightarrow {AM} .\overrightarrow {CN} = 0\cr& \Leftrightarrow \,\,\left( {{2 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} } \right)\left( {{1 \over 3}\overrightarrow {AB} - \overrightarrow {AC} } \right) \cr&\;\;\;\;\;= 0 \cr 
&  \Leftrightarrow \,\,{2 \over 9}A{B^2} - {2 \over 3}\overrightarrow {AB} .\overrightarrow {AC} + {1 \over 9}\overrightarrow {AC} .\,\overrightarrow {AB} - {1 \over 3}A{C^2}\cr&\;\;\;\;\; = 0 \cr 
&  \Leftrightarrow \,\,{2 \over 9}{c^2}  - \frac{2}{3}.0 + \frac{1}{9}.0- {1 \over 3}{b^2} = 0 \cr 
& \ \Leftrightarrow \,\,2{c^2} = 3{b^2} \cr} \)