Bài 17 trang 28 Hình học 12 Nâng cao

Đề bài

Tính thể tích của khối hộp \(ABCD.A'B'C'D'\), biết rằng \(AA'B'D'\) là khối tứ diện đều cạnh \(a\).

Lời giải chi tiết

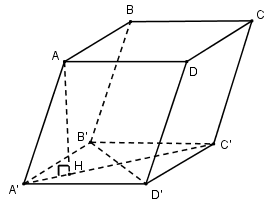
\(AA’B’D’\) là tứ diện đều nên đường cao \(AH\) có \(H\) là tâm của tam giác đều \(A’B’D’\) cạnh \(a\).

Mà \(ABCD)//(A'B'C'D') nên

h=d((ABCD),(A'B'C'D'))=d(A,(A'B'C'D')).

Do đó:

\(\eqalign{
& A'H = {2 \over 3}A'O' = {2 \over 3}{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 3} \cr 
& \Rightarrow A{H^2} = AA{'^2} - A'{H^2} \cr &= {a^2} - {{{a^2}} \over 3} = {{2{a^2}} \over 3} \cr 
& \Rightarrow AH = a\sqrt {{2 \over 3}} = {{a\sqrt 6 } \over 3} \cr} \)

Diện tích tam giác đều \(A’B’D’\) là: \({S_{A'B'D'}}= \frac{1}{2}A'B'.A'D'\sin {60^0} = {{{a^2}\sqrt 3 } \over 4}\)
Diện tích hình thoi \(A’B’C’D’\): \({S_{A'B'C'D'}} = 2{S_{A'B'D'}} = {{{a^2}\sqrt 3 } \over 2}\)
Vậy thể tích khối hộp đã cho là:

\(V = B.h \) \(= {{{a^2}\sqrt 3 } \over 2}.{{a\sqrt 6 } \over 3} = {{{a^3}\sqrt 2 } \over 2}\)