Bài 10 trang 111 SGK Toán 7 tập 1
Giải bài 10 trang 111 SGK Toán 7 tập 1. Trong các hình sau các tam giác nào bằng nhau(Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau).
Đề bài
Trong các hình 63, 64 các tam giác nào bằng nhau (Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó.
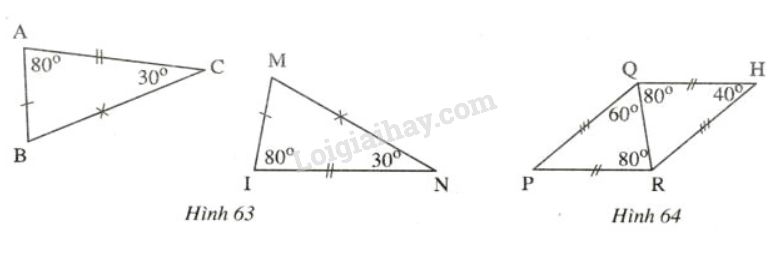
Phương pháp giải - Xem chi tiết
Áp dụng dấu hiệu nhận biết hai đường thẳng song song.
Áp dụng định lí tổng ba góc trong một tam giác.
Áp dụng định nghĩa hai tam giác bằng nhau.
Lời giải chi tiết
Hình 63 ta có:
\(\widehat{A}=\widehat{I}=80^0\),
\(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-(80^0+30^0)=70^0\)
\(AB=IM, AC=IN, BC=MN\).
Suy ra \(∆ABC=∆IMN\)
Hình 64 ta có:
\(\widehat {RQH} = \widehat {QRP} = {80^0}\)
Áp dụng đinh lí tổng các góc của một tam giác vào \(\Delta QHR\) ta có:
\(\eqalign{
& \widehat {QHR} + \widehat {HRQ} + \widehat {RQH} = {180^o} \cr
& \Rightarrow \widehat {HRQ} = {180^o} - \left( {\widehat {QHR} + \widehat {RQH}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\; = {180^o} - \left( {{{40}^o} + {{80}^o}} \right) = {60^o} \cr} \)
\(\Rightarrow \widehat {HRQ} = \widehat {PQR} = {60^o}\)
Áp dụng đinh lí tổng các góc của một tam giác vào \(\Delta PQR\) ta có:
\(\eqalign{
& \widehat {PQR} + \widehat {QRP} + \widehat {RPQ} = {180^o} \cr
& \Rightarrow \widehat {RPQ} = {180^o} - \left( {\widehat {PQR} + \widehat {QRP}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^o} - \left( {{{60}^o} + {{80}^o}} \right) = {40^o} \cr} \)
\( \Rightarrow \widehat {RPQ} = \widehat {QHR} = {40^o}\)
\(QH= RP, HR= PQ, QR=RQ\).
Suy ra \(∆HQR=∆PRQ\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 10 trang 111 SGK Toán 7 tập 1 timdapan.com"







