Ôn tập chương 2 Mặt nón, Mặt trụ, Mặt cầu

- Mặt nón, hình nón, khối nón.

- Mặt trụ, hình trụ, khối trụ.

- Mặt cầu, khối cầu, vị trí tương đối giữa mặt cầu với đường thẳng, mặt phẳng.

a) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

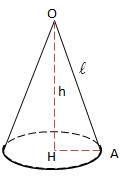
Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

- Thể tích khối nón: 

\(V=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).

- Diện tích xung quanh hình nón: 

\(S_{xq}=\pi Rl\).

- Diện tích toàn phần hình nón: 

\(S_{tp}=\pi Rl+\pi R^{2}\).

b) Các công thức tính toán liên quan đển hình trụ, khối trụ

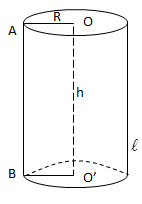
- Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).

- Diện tích xung quanh hình trụ: 

\(S_{xq}=2\pi .R.h\).

- Diện tích toàn phân hình trụ: 

\(S_{tp}=2\pi .R.h+2\pi R^2\).

Trong đó:

+ R: bán kính đáy.

+ h: chiều cao (k/c giữa hai đáy = OO').​

c) Công thức tính toán liên qua đến mặt cầu, khối cầu

- Công thức tính thể tích khối cầu bán kính R: 

\(V=\frac{4}{3}\pi .R^3\).

- Công thức tính diện tích mặt cầu bán kính R: 

\(S = 4\pi {R^2}.\)

3. Bài tập Ôn tập 

Bài tập 1: 

Cho tam giác ABC vuông tại A có AC = 3a, AB = 4a. Cho tam giác này quay quanh đường thẳng BC, tính thể tích V của khối tròn xoay thu được.

Lời giải:

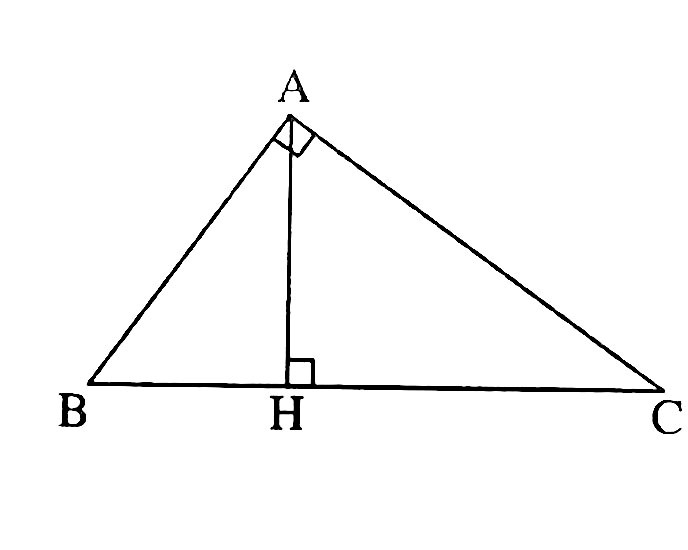
Kẻ đường cao AH của ∆ABC

Khi quay tam giác ABC quanh đường thẳng BC miền tam giác ABC sinh ra hai khối nón chung đáy có bán kính đáy là R = AH và chiều cao lần lượt là HB và HC.

Ta có: 

\({\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{16{a^2}}} + \frac{1}{{9{a^2}}} = \frac{{25}}{{144{a^2}}}.}\)

Suy ra \(A{H^2} = \frac{{25}}{{144{a^2}}}.\)

Mặt khác: 

\(HB + HC = BC = \sqrt {A{B^2} + A{C^2}} = 5a.\)

Thể tích khối tròn xoay sinh ra là:

\({V = {V_1} + {V_2} = \frac{1}{3}\pi A{H^2}.\left( {HB + HC} \right)}\)

\(= \frac{1}{3}\pi .\frac{{144{a^2}}}{{25}}.5a = \frac{{144\pi {a^2}}}{{15}}.\)

Bài tập 2:

Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2m, 3m, 2m lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo hình trụ có chiều cao là 5 cm bà bán kính đường tròn đáy là 4 cm. Trung bình một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi đến ngày thứ bao nhiêu bể sẽ hết nước?

Lời giải:

Thể tích nước được đựng đầy trong hình bể là là thể tích của hình hộp chữ nhật: 

\(V = 2.3.2 = 12\left( {{m^3}} \right).\)

Thể tích nước đựng đầy trong một gáo là: 

\({{V_g} = \pi {4^2}.5 = 80\pi \left( {c{m^3}} \right) = \frac{\pi }{{12500}}\left( {{m^3}} \right).}\)

Mội ngày bể được múc ra 170 gáo nước tức trong một ngày lượng được được lấy ra là: 

\({V_m} = 170.{V_g} = \frac{{17}}{{1250}}\pi \left( {{m^3}} \right)\).

Ta có: \(\frac{V}{{{V_m}}} = \frac{{12}}{{\frac{{17}}{{1250}}\pi }} \simeq 280,8616643\)

Vậy đến ngày thứ 281 bể sẽ hết nước.

Bài tập 3: 

Một quả bóng bàn và một chiếc chén hình trụ có cùng chiều cao. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài của quả bóng có chiều cao bằng \(\frac{3}{4}\) chiều cao của nó. Tìm V₁, V₂ lần lượt là thể tích của quả bóng và chiếc chén. 

Lời giải:

 

Gọi chiều cao của chiếc chén hình trụ là 2h và bán kính đường tròn đáy của hình trụ là r.

Gọi O là tâm của quả bóng bàn, khi đó khoảng cách từ O đến mặt phẳng thiết diện bằng \(\frac{h}{2}\) 

Bán kính đường tròn đáy hình trụ là: 

\(AI = \sqrt {O{A^2} - O{I^2}} = \frac{{h\sqrt 3 }}{2}.\)

Thể tích của quả bóng bàn là: 

\({V_1} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {h^3} = \frac{{4\pi {h^3}}}{3}.\)

Thể tích của chiếc chén là: 

\({{V_2} = \pi {r^2}{h_c} = \pi {{\left( {\frac{{h\sqrt 3 }}{2}} \right)}^2}.2h = \frac{{3\pi {h^3}}}{2}}\)

Bài tập 4:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC = 2a. SA vuông góc (ABC) và \(SA = 2a\sqrt 2\). Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Lời giải:

Gọi M là trung điểm của BC.

Do ABC là tam giác vuông cân tại A nên: 

\(AB = AC = \frac{{BC}}{{\sqrt 2 }} = a\sqrt 2 ;AM = \frac{{BC}}{2} = a\)  

Dựng đường thẳng qua M song song với SA và cắt mặt phẳng trung trực của SA tại 0.

Khi đó O là tâm mặt cầu ngoại tiếp hình chóp.

Do ABCD là hình chữ nhật nên: 

\(OM=AE=a \sqrt 2.\)

Mặc khác:

\(\begin{array}{l}
R = OA = \sqrt {O{M^2} + M{A^2}} \\
 = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}}  = a\sqrt 3 
\end{array}\)

Vậy thể tích khối cầu ngoại tiếp hình chóp là: 

\(V = \frac{4}{3}\pi {R^3} = 4\pi {a^3}\sqrt 3 .\)

- Mặt nón, hình nón, khối nón.

- Mặt trụ, hình trụ, khối trụ.

- Mặt cầu, khối cầu, vị trí tương đối giữa mặt cầu với đường thẳng, mặt phẳng.

a) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

- Thể tích khối nón: 

\(V=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).

- Diện tích xung quanh hình nón: 

\(S_{xq}=\pi Rl\).

- Diện tích toàn phần hình nón: 

\(S_{tp}=\pi Rl+\pi R^{2}\).

b) Các công thức tính toán liên quan đển hình trụ, khối trụ

- Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).

- Diện tích xung quanh hình trụ: 

\(S_{xq}=2\pi .R.h\).

- Diện tích toàn phân hình trụ: 

\(S_{tp}=2\pi .R.h+2\pi R^2\).

Trong đó:

+ R: bán kính đáy.

+ h: chiều cao (k/c giữa hai đáy = OO').​

c) Công thức tính toán liên qua đến mặt cầu, khối cầu

- Công thức tính thể tích khối cầu bán kính R: 

\(V=\frac{4}{3}\pi .R^3\).

- Công thức tính diện tích mặt cầu bán kính R: 

\(S = 4\pi {R^2}.\)

3. Bài tập Ôn tập 

Bài tập 1: 

Cho tam giác ABC vuông tại A có AC = 3a, AB = 4a. Cho tam giác này quay quanh đường thẳng BC, tính thể tích V của khối tròn xoay thu được.

Lời giải:

Kẻ đường cao AH của ∆ABC

Khi quay tam giác ABC quanh đường thẳng BC miền tam giác ABC sinh ra hai khối nón chung đáy có bán kính đáy là R = AH và chiều cao lần lượt là HB và HC.

Ta có: 

\({\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{16{a^2}}} + \frac{1}{{9{a^2}}} = \frac{{25}}{{144{a^2}}}.}\)

Suy ra \(A{H^2} = \frac{{25}}{{144{a^2}}}.\)

Mặt khác: 

\(HB + HC = BC = \sqrt {A{B^2} + A{C^2}} = 5a.\)

Thể tích khối tròn xoay sinh ra là:

\({V = {V_1} + {V_2} = \frac{1}{3}\pi A{H^2}.\left( {HB + HC} \right)}\)

\(= \frac{1}{3}\pi .\frac{{144{a^2}}}{{25}}.5a = \frac{{144\pi {a^2}}}{{15}}.\)

Bài tập 2:

Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2m, 3m, 2m lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo hình trụ có chiều cao là 5 cm bà bán kính đường tròn đáy là 4 cm. Trung bình một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi đến ngày thứ bao nhiêu bể sẽ hết nước?

Lời giải:

Thể tích nước được đựng đầy trong hình bể là là thể tích của hình hộp chữ nhật: 

\(V = 2.3.2 = 12\left( {{m^3}} \right).\)

Thể tích nước đựng đầy trong một gáo là: 

\({{V_g} = \pi {4^2}.5 = 80\pi \left( {c{m^3}} \right) = \frac{\pi }{{12500}}\left( {{m^3}} \right).}\)

Mội ngày bể được múc ra 170 gáo nước tức trong một ngày lượng được được lấy ra là: 

\({V_m} = 170.{V_g} = \frac{{17}}{{1250}}\pi \left( {{m^3}} \right)\).

Ta có: \(\frac{V}{{{V_m}}} = \frac{{12}}{{\frac{{17}}{{1250}}\pi }} \simeq 280,8616643\)

Vậy đến ngày thứ 281 bể sẽ hết nước.

Bài tập 3: 

Một quả bóng bàn và một chiếc chén hình trụ có cùng chiều cao. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài của quả bóng có chiều cao bằng \(\frac{3}{4}\) chiều cao của nó. Tìm V₁, V₂ lần lượt là thể tích của quả bóng và chiếc chén. 

Lời giải:

 

Gọi chiều cao của chiếc chén hình trụ là 2h và bán kính đường tròn đáy của hình trụ là r.

Gọi O là tâm của quả bóng bàn, khi đó khoảng cách từ O đến mặt phẳng thiết diện bằng \(\frac{h}{2}\) 

Bán kính đường tròn đáy hình trụ là: 

\(AI = \sqrt {O{A^2} - O{I^2}} = \frac{{h\sqrt 3 }}{2}.\)

Thể tích của quả bóng bàn là: 

\({V_1} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {h^3} = \frac{{4\pi {h^3}}}{3}.\)

Thể tích của chiếc chén là: 

\({{V_2} = \pi {r^2}{h_c} = \pi {{\left( {\frac{{h\sqrt 3 }}{2}} \right)}^2}.2h = \frac{{3\pi {h^3}}}{2}}\)

Bài tập 4:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC = 2a. SA vuông góc (ABC) và \(SA = 2a\sqrt 2\). Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Lời giải:

Gọi M là trung điểm của BC.

Do ABC là tam giác vuông cân tại A nên: 

\(AB = AC = \frac{{BC}}{{\sqrt 2 }} = a\sqrt 2 ;AM = \frac{{BC}}{2} = a\)  

Dựng đường thẳng qua M song song với SA và cắt mặt phẳng trung trực của SA tại 0.

Khi đó O là tâm mặt cầu ngoại tiếp hình chóp.

Do ABCD là hình chữ nhật nên: 

\(OM=AE=a \sqrt 2.\)

Mặc khác:

\(\begin{array}{l}
R = OA = \sqrt {O{M^2} + M{A^2}} \\
 = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}}  = a\sqrt 3 
\end{array}\)

Vậy thể tích khối cầu ngoại tiếp hình chóp là: 

\(V = \frac{4}{3}\pi {R^3} = 4\pi {a^3}\sqrt 3 .\)