Bài 2: Mặt cầu
Video bài giảng
1. Định nghĩa
- Tập hợp các điểm trong không gian cách điểm O cố định một khoảng không đổi r (r > 0) được gọi là một mặt cầu tâm O bán kính r.
Kí hiệu: \(S\left( {O;r} \right) = \left\{ {M|OM = r} \right\}.\)
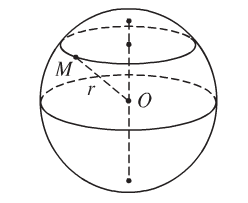
- Đoạn thẳng nối hai điểm nằm trên mặt cầu gọi là dây cung của mặt cầu.
- Dây cung đi qua tâm gọi là đường kính.

- Dây cung CD và đường kính AB.
- Cho mặt cầu S(O;r) và điểm A trong không gian.
+ Nếu OA = r thì điểm A nằm trên mặt cầu.
+ Nếu OA < r thì điểm A nằm trong mặt cầu.
+ Nếu OA > r thì điểm A nằm ngoài mặt cầu.
- Khối cầu: Tập hợp các điểm thuộc mặt cầu S(O;r) cùng với các điểm nằm bên trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O bán kính R.
.png)
2. Tính chất
Nếu điểm A nằm ngoài mặt cầu S(O;r) thì:
- Qua A có vô số tiếp tuyến với mặt cầu.
- Độ dài các đoạn thẳng nối A với các tiếp điểm đều bằng nhau.
- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
.png)
3. Giao của mặt cầu với mặt phẳng
Cho mặt cầu S(O;r) tâm O bán kính r và mặt phẳng (P); H là hình chiếu vuông góc của O lên mặt phẳng (P).
Khi đó h = OH là khoảng cách từ O đến mặt phẳng (P).
- Nếu h = r thì (P) tiếp xúc mặt cầu.
.png)
Ghi nhớ: Điều kiện cần và đủ để mặt phẳng (P) tiếp xúc với mặt cầu S(O;r) tại điểm H là (P) vuông góc với bán kính OH tại điểm H đó.
- Nếu h > r thì (P) không có điểm chung với mặt cầu.
.png)
- Nếu h < r thì (P) cắt mặt cầu S(O;r) theo giao tuyến là một đường tròn tâm H bán kính \(r' = \sqrt {{r^2} - {h^2}} .\)
.png)
4. Giao của mặt cầu với đường thẳng
Cho mặt cầu S(O;r) và đường thẳng ∆. Gọi H là chân đường vuông góc hạ từ O lên ∆, đặt h = OH. Ta có:
- Nếu h = r thì đường thẳng ∆ tiếp xúc với mặt cầu tại H.
.png)
Ghi nhớ: Điều kiện cần và đủ để đường thẳng \(\Delta\) tiếp xúc với mặt cầu S(O;r) tại điểm H là \(\Delta\) vuông góc với bán kính OH tại điểm H đó.
- Nếu h < r, \(\Delta\) cắt mặt cầu S(0;r) tại hai điểm M, N, đoạn thẳng MN có độ dài \(MN=2\sqrt{r^2-h^2}.\)
.png)
- Nếu h > r thì đường thẳng ∆ không cắt mặt cầu.
.png)
5. Công thức diện tích mặt cầu và thể tích hình cầu
- Công thức tính thể tích khối cầu bán kính R:
\(V=\frac{4}{3}\pi .R^3\).
- Công thức tính diện tích mặt cầu bán kính R:
\(S = 4\pi {R^2}.\)
6. Mặt cầu ngoại tiếp lăng trụ và hình chóp
a) Mặt cầu ngoại tiếp hình chóp
(1).png)
- Hình chóp có một mặt cầu ngoại tiếp khi và chỉ khi đáy của hình chóp là đa giác nội tiếp.
- Cách xác định tâm mặt cầu ngoại tiếp hình chóp: Nếu hình chóp có mặt cầu ngoại tiếp thì tâm mặt cầu ngoại tiếp hình chóp chính là giao điểm của mặt phẳng trung trực của một cạnh bên và trục dường tròn ngoại tiếp đa giác đáy.
b) Mặt cầu ngoại tiếp lăng trụ
- Hình lăng trụ có một mặt cầu ngoại tiếp khi và chỉ khi lăng trụ đó là lăng trụ đứng có đáy là đa giác nội tiếp.
- Cách xác định tâm mặt cầu ngoại tiếp lăng trụ: nếu lăng trụ có mặt cầu ngoại tiếp thì tâm đường tròn ngoại tiếp lăng trụ đó chính là trung điểm của đoạn nối tâm 2 đường tròn ngoại tiếp hai đa giác đáy.
7. Bài tập minh họa
Ví dụ 1:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 3a, BC = 4a, SA = 12a và vuông góc với mặt đáy. Tính diện tích và thể tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
Lời giải:
Xét các tam giác SAB, SBC, SDC, SAC đều là những tam giác vuông, và có chung SC là cạnh huyền.
Vậy trung điểm I của SC chính là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Xét tam giác ABC vuông tại B ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = 5a\).
Xét tam giác SAC vuông tại A ta có:
\(SC = \sqrt {S{A^2} + A{C^2}} = 13a\).
Vậy bán kính mặt cầu ngoại tiếp khối chóp là:
\(R=\frac{{13a}}{2}\).
Diện tích mặt cầu là:
\(S = 4\pi {R^2}=169\pi a^2.\)
Thể tích khối cầu là:
\(V=\frac{4}{3}\pi .R^3=\frac{2197}{6}\pi a^3.\)
Ví dụ 2:
Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện đều cạnh a.
Lời giải:
.png)
Gọi H là tâm của tam giác đều BCD.
Dễ thấy A nằm trên trục của đường tròn ngoại tiếp ∆BCD.
Gọi O là tâm của mặt cầu ngoại tiếp ABCD thì O nằm trên AH.
Đặt OH = x (x > 0)
Ta có:
\(BH = \frac{2}{3}BE = \frac{2}{3}a.\sin {60^0}= a.\frac{{\sqrt 3 }}{3}\)
\(AH = \sqrt {A{B^2} - B{H^2}}= \sqrt {{a^2} - \frac{{{a^2}}}{3}} \)
\(= a\sqrt {\frac{2}{3}}\)
\(OA = AH - x = a\sqrt {\frac{2}{3}} - x\)
\(BO = \sqrt {B{H^2} + H{O^2}} = \sqrt {\frac{{{a^2}}}{3} + {x^2}}\)
Mặt khác:
\(\begin{array}{l}
OA = OB \Leftrightarrow a\sqrt {\frac{2}{3}} - x = \sqrt {\frac{{{a^2}}}{3} + {x^2}} \\
\Leftrightarrow x = \frac{{a\sqrt 6 }}{{12}}
\end{array}\)
Vậy tâm O của mặt cầu ngoại tiếp nằm trên AH và cách (BCD) một khoảng \(OH=\frac{{a\sqrt 6 }}{{12}}.\)
Bán kính của mặt cầu là:
\(R = OA = a\sqrt {\frac{2}{3}} - \frac{{a\sqrt 6 }}{{12}} = \frac{{a\sqrt 6 }}{4}.\)
Ví dụ 3:
Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện OABC có OA = a, OB = b, OC = c và OA, OB, OC đôi một vuông góc.
Lời giải:
.png)
Gọi H là trung điểm của AB.
Dễ thấy H là tâm đường tròn ngoại tiếp ∆SAB.
Mặt phẳng trung trực của SC cắt trục đường tròn (SAB) tại O.
Ta có O chính là tâm mặt cầu ngoại tiếp tứ diện SABC.
Do OHSM là hình chữ nhật nên:
\(\begin{array}{l}
MS = OH = \frac{1}{2}c\\
R = SO = \sqrt {S{H^2} + H{O^2}} \\
= \sqrt {\frac{{A{B^2}}}{4} + H{O^2}} \\
= \sqrt {\frac{{S{A^2} + S{B^2}}}{4} + H{O^2}} = \frac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}
\end{array}\)
Ví dụ 4:
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy là a, góc giữa AB’ với mặt đáy là 450. Tính diện tích mặt cầu ngoại tiếp lăng trụ.
Lời giải:
\(B'B = AB.\tan {45^0} = a\).
Gọi O, O’ lần lượt là trọng tâm các tam giác đều ABC và A’B’C’.
Tâm mặt cầu ngoại tiếp khối lăng trụ là trung điểm I của OO’.
Do A'B'C' là tam giác đều nên:
\(O'C'=\frac{a \sqrt3}{3},\,IO'=\frac{1}{2}BB'=\frac{a}{2}.\)
Suy ra:
\(\begin{array}{l}
R = IC' = \sqrt {IO{'^2} + O'C{'^2}} \\
= \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt {21} }}{6}
\end{array}\)
Vậy diện tích mặt cầu là:
\(S = 4\pi {R^2} = \frac{7}{3}\pi {a^2}\).
1. Định nghĩa
- Tập hợp các điểm trong không gian cách điểm O cố định một khoảng không đổi r (r > 0) được gọi là một mặt cầu tâm O bán kính r.
Kí hiệu: \(S\left( {O;r} \right) = \left\{ {M|OM = r} \right\}.\)

- Đoạn thẳng nối hai điểm nằm trên mặt cầu gọi là dây cung của mặt cầu.
- Dây cung đi qua tâm gọi là đường kính.

- Dây cung CD và đường kính AB.
- Cho mặt cầu S(O;r) và điểm A trong không gian.
+ Nếu OA = r thì điểm A nằm trên mặt cầu.
+ Nếu OA < r thì điểm A nằm trong mặt cầu.
+ Nếu OA > r thì điểm A nằm ngoài mặt cầu.
- Khối cầu: Tập hợp các điểm thuộc mặt cầu S(O;r) cùng với các điểm nằm bên trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O bán kính R.
.png)
2. Tính chất
Nếu điểm A nằm ngoài mặt cầu S(O;r) thì:
- Qua A có vô số tiếp tuyến với mặt cầu.
- Độ dài các đoạn thẳng nối A với các tiếp điểm đều bằng nhau.
- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
.png)
3. Giao của mặt cầu với mặt phẳng
Cho mặt cầu S(O;r) tâm O bán kính r và mặt phẳng (P); H là hình chiếu vuông góc của O lên mặt phẳng (P).
Khi đó h = OH là khoảng cách từ O đến mặt phẳng (P).
- Nếu h = r thì (P) tiếp xúc mặt cầu.
.png)
Ghi nhớ: Điều kiện cần và đủ để mặt phẳng (P) tiếp xúc với mặt cầu S(O;r) tại điểm H là (P) vuông góc với bán kính OH tại điểm H đó.
- Nếu h > r thì (P) không có điểm chung với mặt cầu.
.png)
- Nếu h < r thì (P) cắt mặt cầu S(O;r) theo giao tuyến là một đường tròn tâm H bán kính \(r' = \sqrt {{r^2} - {h^2}} .\)
.png)
4. Giao của mặt cầu với đường thẳng
Cho mặt cầu S(O;r) và đường thẳng ∆. Gọi H là chân đường vuông góc hạ từ O lên ∆, đặt h = OH. Ta có:
- Nếu h = r thì đường thẳng ∆ tiếp xúc với mặt cầu tại H.
.png)
Ghi nhớ: Điều kiện cần và đủ để đường thẳng \(\Delta\) tiếp xúc với mặt cầu S(O;r) tại điểm H là \(\Delta\) vuông góc với bán kính OH tại điểm H đó.
- Nếu h < r, \(\Delta\) cắt mặt cầu S(0;r) tại hai điểm M, N, đoạn thẳng MN có độ dài \(MN=2\sqrt{r^2-h^2}.\)
.png)
- Nếu h > r thì đường thẳng ∆ không cắt mặt cầu.
.png)
5. Công thức diện tích mặt cầu và thể tích hình cầu
- Công thức tính thể tích khối cầu bán kính R:
\(V=\frac{4}{3}\pi .R^3\).
- Công thức tính diện tích mặt cầu bán kính R:
\(S = 4\pi {R^2}.\)
6. Mặt cầu ngoại tiếp lăng trụ và hình chóp
a) Mặt cầu ngoại tiếp hình chóp
(1).png)
- Hình chóp có một mặt cầu ngoại tiếp khi và chỉ khi đáy của hình chóp là đa giác nội tiếp.
- Cách xác định tâm mặt cầu ngoại tiếp hình chóp: Nếu hình chóp có mặt cầu ngoại tiếp thì tâm mặt cầu ngoại tiếp hình chóp chính là giao điểm của mặt phẳng trung trực của một cạnh bên và trục dường tròn ngoại tiếp đa giác đáy.
b) Mặt cầu ngoại tiếp lăng trụ
- Hình lăng trụ có một mặt cầu ngoại tiếp khi và chỉ khi lăng trụ đó là lăng trụ đứng có đáy là đa giác nội tiếp.
- Cách xác định tâm mặt cầu ngoại tiếp lăng trụ: nếu lăng trụ có mặt cầu ngoại tiếp thì tâm đường tròn ngoại tiếp lăng trụ đó chính là trung điểm của đoạn nối tâm 2 đường tròn ngoại tiếp hai đa giác đáy.
7. Bài tập minh họa
Ví dụ 1:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 3a, BC = 4a, SA = 12a và vuông góc với mặt đáy. Tính diện tích và thể tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
Lời giải:
Xét các tam giác SAB, SBC, SDC, SAC đều là những tam giác vuông, và có chung SC là cạnh huyền.
Vậy trung điểm I của SC chính là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Xét tam giác ABC vuông tại B ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = 5a\).
Xét tam giác SAC vuông tại A ta có:
\(SC = \sqrt {S{A^2} + A{C^2}} = 13a\).
Vậy bán kính mặt cầu ngoại tiếp khối chóp là:
\(R=\frac{{13a}}{2}\).
Diện tích mặt cầu là:
\(S = 4\pi {R^2}=169\pi a^2.\)
Thể tích khối cầu là:
\(V=\frac{4}{3}\pi .R^3=\frac{2197}{6}\pi a^3.\)
Ví dụ 2:
Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện đều cạnh a.
Lời giải:
.png)
Gọi H là tâm của tam giác đều BCD.
Dễ thấy A nằm trên trục của đường tròn ngoại tiếp ∆BCD.
Gọi O là tâm của mặt cầu ngoại tiếp ABCD thì O nằm trên AH.
Đặt OH = x (x > 0)
Ta có:
\(BH = \frac{2}{3}BE = \frac{2}{3}a.\sin {60^0}= a.\frac{{\sqrt 3 }}{3}\)
\(AH = \sqrt {A{B^2} - B{H^2}}= \sqrt {{a^2} - \frac{{{a^2}}}{3}} \)
\(= a\sqrt {\frac{2}{3}}\)
\(OA = AH - x = a\sqrt {\frac{2}{3}} - x\)
\(BO = \sqrt {B{H^2} + H{O^2}} = \sqrt {\frac{{{a^2}}}{3} + {x^2}}\)
Mặt khác:
\(\begin{array}{l}
OA = OB \Leftrightarrow a\sqrt {\frac{2}{3}} - x = \sqrt {\frac{{{a^2}}}{3} + {x^2}} \\
\Leftrightarrow x = \frac{{a\sqrt 6 }}{{12}}
\end{array}\)
Vậy tâm O của mặt cầu ngoại tiếp nằm trên AH và cách (BCD) một khoảng \(OH=\frac{{a\sqrt 6 }}{{12}}.\)
Bán kính của mặt cầu là:
\(R = OA = a\sqrt {\frac{2}{3}} - \frac{{a\sqrt 6 }}{{12}} = \frac{{a\sqrt 6 }}{4}.\)
Ví dụ 3:
Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện OABC có OA = a, OB = b, OC = c và OA, OB, OC đôi một vuông góc.
Lời giải:
.png)
Gọi H là trung điểm của AB.
Dễ thấy H là tâm đường tròn ngoại tiếp ∆SAB.
Mặt phẳng trung trực của SC cắt trục đường tròn (SAB) tại O.
Ta có O chính là tâm mặt cầu ngoại tiếp tứ diện SABC.
Do OHSM là hình chữ nhật nên:
\(\begin{array}{l}
MS = OH = \frac{1}{2}c\\
R = SO = \sqrt {S{H^2} + H{O^2}} \\
= \sqrt {\frac{{A{B^2}}}{4} + H{O^2}} \\
= \sqrt {\frac{{S{A^2} + S{B^2}}}{4} + H{O^2}} = \frac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}
\end{array}\)
Ví dụ 4:
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy là a, góc giữa AB’ với mặt đáy là 450. Tính diện tích mặt cầu ngoại tiếp lăng trụ.
Lời giải:
\(B'B = AB.\tan {45^0} = a\).
Gọi O, O’ lần lượt là trọng tâm các tam giác đều ABC và A’B’C’.
Tâm mặt cầu ngoại tiếp khối lăng trụ là trung điểm I của OO’.
Do A'B'C' là tam giác đều nên:
\(O'C'=\frac{a \sqrt3}{3},\,IO'=\frac{1}{2}BB'=\frac{a}{2}.\)
Suy ra:
\(\begin{array}{l}
R = IC' = \sqrt {IO{'^2} + O'C{'^2}} \\
= \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt {21} }}{6}
\end{array}\)
Vậy diện tích mặt cầu là:
\(S = 4\pi {R^2} = \frac{7}{3}\pi {a^2}\).
.PNG)
.PNG)
.PNG)