Bài 1: Khái niệm về mặt tròn xoay
Video bài giảng
1. Mặt nón - Hình nón - Khối nón
a) Mặt nón
Trong không gian cho hai đường thẳng \(\Delta\) và \(l\) cắt nhau tại O sao cho:
\((\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).\)
Cho \(l\) quay quanh \(\Delta\) ta được mặt nón tròn xoay có:
- \(l\): đường sinh.
- \(\Delta\): trục của mặt nón.
- \(O=l\cap \Delta\): đỉnh của mặt nón.
- \(2\alpha :\) góc ở đỉnh.
.png)
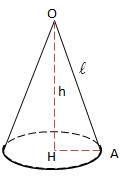
b) Hình nón
Cắt mặt nón tròn xoay đỉnh O, trục \(\Delta\) bởi mặt phẳng (P) sao cho:
\((P)\perp \Delta ,O\notin (P).\)
Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.
c) Khối nón
Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:
- Thể tích khối nón:
\(V=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).
- Diện tích xung quanh hình nón:
\(S_{xq}=\pi Rl\).
- Diện tích toàn phần hình nón:
\(S_{tp}=\pi Rl+\pi R^{2}\).
2. Mặt trụ - Hình trụ - Khối trụ
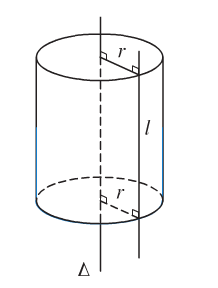
a) Mặt trụ
Trong không gian, cho đường thẳng \(l\) song song và cách đường thẳng \(\Delta\) một khoảng R.
Cho \(l\) quay quanh \(\Delta\) ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:
- \(l\) là đường sinh.
- \(\Delta\) là trục mặt trụ.
- \(R\) là bán kính mặt trụ.
b) Hình trụ
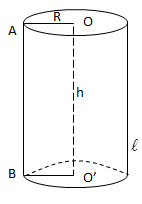
Xét hình chữ nhật OABO'.
Cho đường gấp khúc OABO' quay quanh OO' ta được hình trụ tròn xoay:
- OA: Bán kính đường tròn đáy.
- AB: đường sinh.
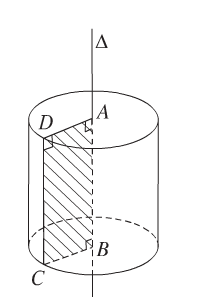
c) Khối trụ
Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.
d) Các công thức tính toán liên quan đển hình trụ, khối trụ

- Thể tích khối trụ: \(V=\pi .R^2.h\) (= Sđáy.h).
- Diện tích xung quanh hình trụ:
\(S_{xq}=2\pi .R.h\).
- Diện tích toàn phân hình trụ:
\(S_{tp}=2\pi .R.h+2\pi R^2\).
Trong đó:
- R: bán kính đáy.
- h: chiều cao (k/c giữa hai đáy = OO').
3. Bài tập liên quan đến mặt nón - hình nón -khối nón
Ví dụ 1:
Trong không gian cho tam giác ABC vuông tại A có AB=a, AC = 2a. Quay tam giác ABC xung quanh cạnh AB ta được một khối nón. Tính thể tích V của khối nón đó.
Lời giải:
.jpg)
Hình nón thu được có bán kính đáy R = AC = 2a, chiều cao h = AB = a.
Vậy thể tích khối nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{{4\pi {a^3}}}{3}.\)
Ví dụ 2:
Trong không gian cho tam giác ABC vuông tại A có có AB = 5, AC = 12. Cho đường gấp khúc BAC quay quanh cạnh BC ta được hình nón tròn xoay. Tính thể tích của khối nón đó.
Lời giải:
Khi quay đường gấp khúc BAC quay quanh cạnh BC ta được hai hình nón:
Hình nón thứ nhất có đường cao \({h_1} = BH\), Bán kính đáy \({R_1} = AH\).
Hình nón thứ hau có đường cao \({h_2} = CH\), Bán kính đáy \({R_2} = AH\).
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{60}}{{13}}\)
\(BC = \sqrt {A{B^2} + A{C^2}} = 13\)
Vậy thể tích khối tròn xoay thu được là:
\(\begin{array}{l}
V = \frac{1}{3}\pi {R_1}^2{h_1} + \frac{1}{3}\pi R_2^2{h_2}\\
= \frac{1}{3}\pi A{H^2}(BH + CH) = \frac{{1200}}{{13}}\pi .
\end{array}\)
Ví dụ 3:
Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a.
a) Tính diện tích xung quanh và diện tích toàn phần của hình nón.
b) Tính thể tích của khối nó.
c) Một thiết diện qua đỉnh tạo với đáy một góc 600. Tính diện tích của thiết diện này.
Lời giải:
.png)
a) Thiết diện qua trục là tam giác SAB vuông cân tại S nên: \(\widehat A = \widehat B = {45^0}.\)
Diện tích xung quanh hình nón là:
\(\begin{array}{l}
{S_{xq}} = \pi Rl = \pi .OA.SA\\
= \pi .\frac{a}{{\sqrt 2 }}.a = \frac{{\pi {a^2}}}{{\sqrt 2 }}.
\end{array}\)
Diện tích toàn phần hình nón là:
\(\begin{array}{l}
{S_{tp}} = {S_{xq}} + {S_{day}} = \frac{{\pi {a^2}}}{{\sqrt 2 }} + \frac{{\pi {a^2}}}{2}\\
= \left( {\frac{1}{{\sqrt 2 }} + \frac{1}{2}} \right)\pi {a^2}.
\end{array}\)
b) Thể tích khối nón là:
\(\begin{array}{l}
V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O{A^2}.SO\\
= \frac{1}{3}\pi .\frac{{{a^2}}}{2}.\frac{a}{{\sqrt 2 }} = \frac{{\pi {a^3}}}{{6\sqrt 2 }}.
\end{array}\)
c) Thiết diện (SAC) qua đỉnh tạo với đáy một góc 600.
Kẻ \(OM \bot AC \Rightarrow SM \bot AC \Rightarrow \widehat {SMO} = {60^0}.\)
Do tam giác SMO vuông tại O nên \(OM = \frac{{SO}}{{\tan 60}} = \frac{{a\sqrt 6 }}{6}.\)
Tam giác OAM vuông tại M nên: \(AM = \sqrt {O{A^2} - O{M^2}} = \frac{{a\sqrt 3 }}{3}\).
Tam giác ABC vuông tại C (nội tiếp đường tròn) suy ra \(BC \bot AC.\)
Suy ra OM là đường trung bình của tam giác ABC.
Nên \(AC = 2AM = \frac{{2a\sqrt 3 }}{3}.\)
Ta có: \(SM = SO.\sin {60^0} = \frac{{a\sqrt 6 }}{3}.\)
Vậy diện tích thiết diện là:
\(\begin{array}{l}
{S_{SAC}} = \frac{1}{2}.SM.AC\\
= \frac{1}{2}.\frac{{a\sqrt 6 }}{3}.\frac{{2a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 2 }}{3}.
\end{array}\)
4. Bài tập liên quan đến mặt trụ - hình trụ - khối trụ
Ví dụ 1:
Cho hình chữ nhật ABCD có AB = 2AD. Gọi V1 là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB và V2 là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD. Tính tỉ số \(\frac{V_2}{V_1}\).
Lời giải:
.png)
Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB có bán kính đáy AD, chiều cao AB: \({V_1} = AB.\left( {\pi A{D^2}} \right)\)
Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD có bán kính đáy AB, chiều cao AD: \({V_2} = AD.\left( {\pi A{B^2}} \right)\)
Vậy: \(\frac{{{V_2}}}{{{V_1}}} = \frac{{AD.\left( {\pi A{B^2}} \right)}}{{AB.\left( {\pi A{D^2}} \right)}} = \frac{{AB}}{{AD}} = 2.\)
Ví dụ 2:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính diện tích xung quanh S của hình trụ tròn xoay ngoại tiếp lăng trụ.
Lời giải:
.png)
Diện tích xung quanh mặt trụ được tính theo công thức \({S_{xq}} = 2\pi .R.l\).
Gọi R là bán kính đường tròn ngoại tiếp \(\Delta ABC\).
\(\Rightarrow R = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\); \(l =AA'=a\).
Vậy diện tích cần tìm là:
\({S_{xq}} = 2\pi .\frac{{a\sqrt 3 }}{3}.a = 2\pi \frac{{{a^2}\sqrt 3 }}{3}\) (đvdt).
Ví dụ 6:
Một hình trụ có bán kính đáy R = 5 cm và khoảng cách giữa hai đáy bằng 7 cm.
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) Tính thể tích của khối trụ
c) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Hãy tính diện tích của thiết diện được tạo nên.
Lời giải:
.png)
Hình trụ có bán kính đáy R = 5 và chiều cao h = 7.
a) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi Rl = 2\pi .5.7 = 70\pi \,\,(c{m^2})\)
Diện tích toàn phần hình trụ là:
\({S_{tp}} = {S_{xq}} + 2.{S_{day}} = 70\pi + 2\pi {.5^2} \)
\(= 120\pi \,\,(c{m^2}).\)
b) Thể tích khối trụ là:
\(V = \pi {R^2}h = \pi {.5^2}.7 = 175\pi \,\,(c{m^3}).\)
c) Gọi I là trung điểm của AB suy ra OI=3cm.
\(IB = \sqrt {O{B^2} - O{I^2}} = \sqrt {{5^2} - {3^2}} = 4.\)
Ta có: AB = 2IB = 8.
Dễ thấy thiết diện ABB'A' là hình chữ nhật.
Vậy diện tích thiết diện là:
\({S_{ABB'A'}} = AB.AA' = 8.7 = 56\,\,(c{m^2}).\)
1. Mặt nón - Hình nón - Khối nón
a) Mặt nón
Trong không gian cho hai đường thẳng \(\Delta\) và \(l\) cắt nhau tại O sao cho:
\((\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).\)
Cho \(l\) quay quanh \(\Delta\) ta được mặt nón tròn xoay có:
- \(l\): đường sinh.
- \(\Delta\): trục của mặt nón.
- \(O=l\cap \Delta\): đỉnh của mặt nón.
- \(2\alpha :\) góc ở đỉnh.
.png)
b) Hình nón
Cắt mặt nón tròn xoay đỉnh O, trục \(\Delta\) bởi mặt phẳng (P) sao cho:
\((P)\perp \Delta ,O\notin (P).\)
Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.

c) Khối nón
Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:
- Thể tích khối nón:
\(V=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).
- Diện tích xung quanh hình nón:
\(S_{xq}=\pi Rl\).
- Diện tích toàn phần hình nón:
\(S_{tp}=\pi Rl+\pi R^{2}\).
2. Mặt trụ - Hình trụ - Khối trụ
a) Mặt trụ
Trong không gian, cho đường thẳng \(l\) song song và cách đường thẳng \(\Delta\) một khoảng R.
Cho \(l\) quay quanh \(\Delta\) ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:
- \(l\) là đường sinh.
- \(\Delta\) là trục mặt trụ.
- \(R\) là bán kính mặt trụ.

b) Hình trụ

Xét hình chữ nhật OABO'.
Cho đường gấp khúc OABO' quay quanh OO' ta được hình trụ tròn xoay:
- OA: Bán kính đường tròn đáy.
- AB: đường sinh.
c) Khối trụ
Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.

d) Các công thức tính toán liên quan đển hình trụ, khối trụ

- Thể tích khối trụ: \(V=\pi .R^2.h\) (= Sđáy.h).
- Diện tích xung quanh hình trụ:
\(S_{xq}=2\pi .R.h\).
- Diện tích toàn phân hình trụ:
\(S_{tp}=2\pi .R.h+2\pi R^2\).
Trong đó:
- R: bán kính đáy.
- h: chiều cao (k/c giữa hai đáy = OO').
3. Bài tập liên quan đến mặt nón - hình nón -khối nón
Ví dụ 1:
Trong không gian cho tam giác ABC vuông tại A có AB=a, AC = 2a. Quay tam giác ABC xung quanh cạnh AB ta được một khối nón. Tính thể tích V của khối nón đó.
Lời giải:
.jpg)
Hình nón thu được có bán kính đáy R = AC = 2a, chiều cao h = AB = a.
Vậy thể tích khối nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{{4\pi {a^3}}}{3}.\)
Ví dụ 2:
Trong không gian cho tam giác ABC vuông tại A có có AB = 5, AC = 12. Cho đường gấp khúc BAC quay quanh cạnh BC ta được hình nón tròn xoay. Tính thể tích của khối nón đó.
Lời giải:
Khi quay đường gấp khúc BAC quay quanh cạnh BC ta được hai hình nón:
Hình nón thứ nhất có đường cao \({h_1} = BH\), Bán kính đáy \({R_1} = AH\).
Hình nón thứ hau có đường cao \({h_2} = CH\), Bán kính đáy \({R_2} = AH\).
Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{60}}{{13}}\)
\(BC = \sqrt {A{B^2} + A{C^2}} = 13\)
Vậy thể tích khối tròn xoay thu được là:
\(\begin{array}{l}
V = \frac{1}{3}\pi {R_1}^2{h_1} + \frac{1}{3}\pi R_2^2{h_2}\\
= \frac{1}{3}\pi A{H^2}(BH + CH) = \frac{{1200}}{{13}}\pi .
\end{array}\)
Ví dụ 3:
Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a.
a) Tính diện tích xung quanh và diện tích toàn phần của hình nón.
b) Tính thể tích của khối nó.
c) Một thiết diện qua đỉnh tạo với đáy một góc 600. Tính diện tích của thiết diện này.
Lời giải:
.png)
a) Thiết diện qua trục là tam giác SAB vuông cân tại S nên: \(\widehat A = \widehat B = {45^0}.\)
Diện tích xung quanh hình nón là:
\(\begin{array}{l}
{S_{xq}} = \pi Rl = \pi .OA.SA\\
= \pi .\frac{a}{{\sqrt 2 }}.a = \frac{{\pi {a^2}}}{{\sqrt 2 }}.
\end{array}\)
Diện tích toàn phần hình nón là:
\(\begin{array}{l}
{S_{tp}} = {S_{xq}} + {S_{day}} = \frac{{\pi {a^2}}}{{\sqrt 2 }} + \frac{{\pi {a^2}}}{2}\\
= \left( {\frac{1}{{\sqrt 2 }} + \frac{1}{2}} \right)\pi {a^2}.
\end{array}\)
b) Thể tích khối nón là:
\(\begin{array}{l}
V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O{A^2}.SO\\
= \frac{1}{3}\pi .\frac{{{a^2}}}{2}.\frac{a}{{\sqrt 2 }} = \frac{{\pi {a^3}}}{{6\sqrt 2 }}.
\end{array}\)
c) Thiết diện (SAC) qua đỉnh tạo với đáy một góc 600.
Kẻ \(OM \bot AC \Rightarrow SM \bot AC \Rightarrow \widehat {SMO} = {60^0}.\)
Do tam giác SMO vuông tại O nên \(OM = \frac{{SO}}{{\tan 60}} = \frac{{a\sqrt 6 }}{6}.\)
Tam giác OAM vuông tại M nên: \(AM = \sqrt {O{A^2} - O{M^2}} = \frac{{a\sqrt 3 }}{3}\).
Tam giác ABC vuông tại C (nội tiếp đường tròn) suy ra \(BC \bot AC.\)
Suy ra OM là đường trung bình của tam giác ABC.
Nên \(AC = 2AM = \frac{{2a\sqrt 3 }}{3}.\)
Ta có: \(SM = SO.\sin {60^0} = \frac{{a\sqrt 6 }}{3}.\)
Vậy diện tích thiết diện là:
\(\begin{array}{l}
{S_{SAC}} = \frac{1}{2}.SM.AC\\
= \frac{1}{2}.\frac{{a\sqrt 6 }}{3}.\frac{{2a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 2 }}{3}.
\end{array}\)
4. Bài tập liên quan đến mặt trụ - hình trụ - khối trụ
Ví dụ 1:
Cho hình chữ nhật ABCD có AB = 2AD. Gọi V1 là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB và V2 là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD. Tính tỉ số \(\frac{V_2}{V_1}\).
Lời giải:
.png)
Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB có bán kính đáy AD, chiều cao AB: \({V_1} = AB.\left( {\pi A{D^2}} \right)\)
Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD có bán kính đáy AB, chiều cao AD: \({V_2} = AD.\left( {\pi A{B^2}} \right)\)
Vậy: \(\frac{{{V_2}}}{{{V_1}}} = \frac{{AD.\left( {\pi A{B^2}} \right)}}{{AB.\left( {\pi A{D^2}} \right)}} = \frac{{AB}}{{AD}} = 2.\)
Ví dụ 2:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính diện tích xung quanh S của hình trụ tròn xoay ngoại tiếp lăng trụ.
Lời giải:
.png)
Diện tích xung quanh mặt trụ được tính theo công thức \({S_{xq}} = 2\pi .R.l\).
Gọi R là bán kính đường tròn ngoại tiếp \(\Delta ABC\).
\(\Rightarrow R = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\); \(l =AA'=a\).
Vậy diện tích cần tìm là:
\({S_{xq}} = 2\pi .\frac{{a\sqrt 3 }}{3}.a = 2\pi \frac{{{a^2}\sqrt 3 }}{3}\) (đvdt).
Ví dụ 6:
Một hình trụ có bán kính đáy R = 5 cm và khoảng cách giữa hai đáy bằng 7 cm.
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) Tính thể tích của khối trụ
c) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Hãy tính diện tích của thiết diện được tạo nên.
Lời giải:
.png)
Hình trụ có bán kính đáy R = 5 và chiều cao h = 7.
a) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi Rl = 2\pi .5.7 = 70\pi \,\,(c{m^2})\)
Diện tích toàn phần hình trụ là:
\({S_{tp}} = {S_{xq}} + 2.{S_{day}} = 70\pi + 2\pi {.5^2} \)
\(= 120\pi \,\,(c{m^2}).\)
b) Thể tích khối trụ là:
\(V = \pi {R^2}h = \pi {.5^2}.7 = 175\pi \,\,(c{m^3}).\)
c) Gọi I là trung điểm của AB suy ra OI=3cm.
\(IB = \sqrt {O{B^2} - O{I^2}} = \sqrt {{5^2} - {3^2}} = 4.\)
Ta có: AB = 2IB = 8.
Dễ thấy thiết diện ABB'A' là hình chữ nhật.
Vậy diện tích thiết diện là:
\({S_{ABB'A'}} = AB.AA' = 8.7 = 56\,\,(c{m^2}).\)
.PNG)