Ôn tập chương 3 Phương pháp toạ độ trong không gian

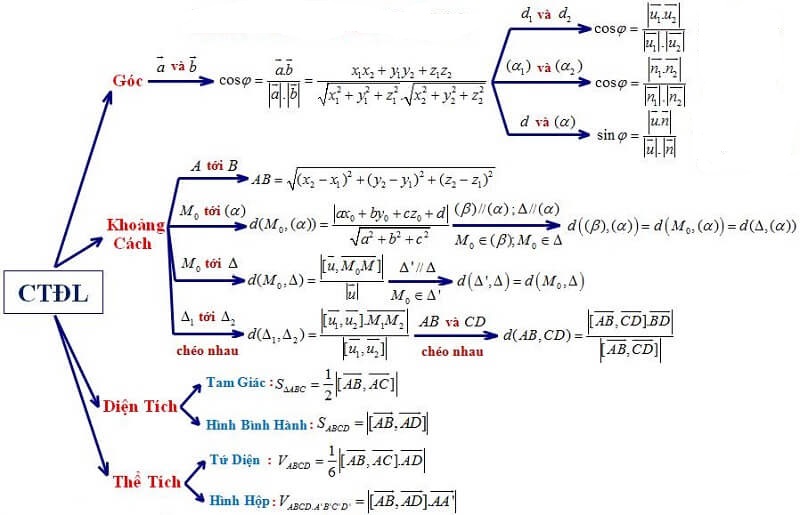
3. Bài tập Ôn tập 

Bài tập 1:

Trong không gian với hệ tọa độ Oxyz , cho A(0;-3;-1) và B(-4;1;-3) và mặt phẳng \((P):x-2y+2z-7=0\).

a) Viết phương trình mặt phẳng (Q) đi qua gốc tọa độ, song song với AB và vuông góc với (P).

b) Lập phương trình mặt cầu nhận đoạn thẳng AB là đường kính.

Lời giải:

a) Ta có 

\(\overrightarrow{AB}=(-4;4;-2),\vec{n}=(1;-2;2)\) là véc tơ pháp tuyến của mặt phẳng (P).

\(\left [ \overrightarrow{AB};\vec{n} \right ]=(4;6;4)\)

(Q) là mặt phẳng đi qua gốc tọa độ O(0;0;0), (Q) song song với AB và vuông góc với mặt phẳng (P) suy ra mặt phẳng (Q) nhận 

\(\overrightarrow {{n_{(Q)}}} = \frac{1}{2}\left[ {\overrightarrow {AB} ;\vec n} \right] = (2;3;2)\) làm VTPT.

Vậy phương trình mặt phẳng (Q) là: 

\(2x+3y+2z=0.\)

b. \(\overrightarrow{AB}=(-4;4;-2)\)

\(\Rightarrow AB=\sqrt{16+16+4}=6\)

Trung điểm AB là \(I(-2;-1;-2)\).

Mặt cầu (S) có tâm I, bán kính \(R=\frac{AB}{2}=3\) có phương trình là:

\((S):(x+2)^2+(y+1)^2+(z+2)^2=9\).

Bài tập 2: 

Cho mặt cầu 

\((S): x^2+y^2+z^2-2x+6y+4z-22=0\) 

và \((\alpha ):x+2y-2z-8=0\).

CRM: \((\alpha )\) cắt (S) theo một đường tròn. Xác định tâm, bán kính đường tròn đó.

Lời giải:

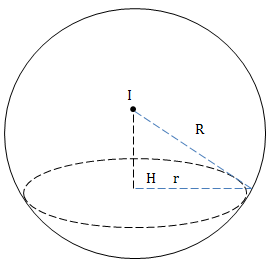
Nhận xét:
Tâm đường tròn giao tuyến của mặt cầu S(I;R) và \((\alpha )\) là hình chiếu của I trên \((\alpha )\) với \(r^2+d^2(I;(\alpha ))=R^2\).

\((S): (x-1)^2+(y+3)^2+(z+2)^2=36\)

Mặt cầu (S) có tâm I(1;-3;-2), bán kính R = 6.

\(d(I;(\alpha ))=\frac{\left | 1-6+4-8 \right |}{\sqrt{1^2+2^2+(-2)^2}}=\frac{9}{3}=3\) Vậy \((\alpha )\) cắt mặt cầu theo 1 đường tròn.

* Xác định tâm của H của đường tròn giao tuyến

Ta có H là hình chiếu của I trên \((\alpha )\).

Đường thẳng \(\Delta\) đi qua I và vuông góc với  \((\alpha )\), tức là nhận \(\vec{n_\alpha }=(1;2;-2)\) làm một VTCP có phương trình là:

\(\Delta \left\{\begin{matrix} x=1+t\\ y=-3+2t\\ z=-2-2t \end{matrix}\right.\)

\(H =\Delta \cap (\alpha )\)

\(H\in \Delta \Rightarrow H(1+t;-3+2t;-2-2t)\)

\(H\in (\alpha ) suy ra:

\(1+t+2(-3+2t)-2(-2-2t)-8=0\)

\(\Leftrightarrow 9t-9=0\Leftrightarrow t=1\)

Suy ra tọa độ H(2;-1;-4).

Bán kính đường trình giao tuyến: 

\(r^2=R^2-IH^2=36-9=27.\)

Vậy \(r=3\sqrt{3}.\)

Bài tập 3:

Cho đường thẳng \(d:\frac{x-12}{4}=\frac{y-9}{3}=\frac{z-1}{1}\) 

và \((P):3x+5y-z-2=0\)

a) Tìm tọa độ giao điểm A của d và (P).

b) Viết phương trình (Q) đi qua M₀(1;2;-1) và vuông góc với d.

c) Tìm tọa độ B' đối xứng với B(1;0;-1) qua (P).

Lời giải:

a) \(A=d\cap (P)\)

\(A\in d\left\{\begin{matrix} x=12+4t\\ y=9+3t\\ z=1+t \end{matrix}\right. \)

\(\Rightarrow A(12+4t;9+3t;1+t)\)

\(A\in (P)\) suy ra:

\(3(12+4t)+5(9+3t)-(1+t)-2=0\)

\(\Leftrightarrow 26t +78=0\Leftrightarrow t=-3\)

Vậy tọa độ là A(0;0;-2).

b) \((Q)\perp d\) nên (Q) nhận 

\(\vec{u_d}=(4;3;1)\) làm một VTPT.

Phương trình mặt phẳng (Q) là:

\((Q):4(x-1)+3(y-2)+1(z+1)=0\) 

Hay \(4x+3y+z-9=0.\)

c) Viết phương trình \(\Delta\) đi qua B và vuông góc (P)

\(\Delta\) \(\perp\) (P) nên \(\Delta\) nhận \(\vec{n_P}=(3;5;-1)\) làm một VTCP.

Phương trình tham số của \(\Delta: \)

\(\left\{\begin{matrix} x=1+3t\\ y=5t\\ z=-1-t \end{matrix}\right.\)

H là hình chiếu của B trên (P)

\(H=\Delta \cap (P)\)

\(H\in \Delta \Rightarrow H(1+3t;5t;-1-t)\)

\(H\in(P)\) suy ra:

\(3(1+3t)+25t+1+t-2=0\)

\(\Leftrightarrow 35t+2=0\)

\(\Leftrightarrow t=-\frac{2}{35}\)

\(H\left ( \frac{29}{35};-\frac{2}{7};-\frac{33}{35} \right )\)

H là trung điểm BB' nên: \(\left\{\begin{matrix} x_{B'}=2x_H-x_B=\frac{23}{35}\\ \\ y_{B'}=2y_H-y_B=-\frac{4}{7}\\ \\ z_{B'}=2z_H-z_B=\frac{2}{35} \end{matrix}\right.\)

Vậy tọa độ \(B' \left ( \frac{23}{35};-\frac{4}{7};\frac{2}{35} \right ).\)

3. Bài tập Ôn tập 

Bài tập 1:

Trong không gian với hệ tọa độ Oxyz , cho A(0;-3;-1) và B(-4;1;-3) và mặt phẳng \((P):x-2y+2z-7=0\).

a) Viết phương trình mặt phẳng (Q) đi qua gốc tọa độ, song song với AB và vuông góc với (P).

b) Lập phương trình mặt cầu nhận đoạn thẳng AB là đường kính.

Lời giải:

a) Ta có 

\(\overrightarrow{AB}=(-4;4;-2),\vec{n}=(1;-2;2)\) là véc tơ pháp tuyến của mặt phẳng (P).

\(\left [ \overrightarrow{AB};\vec{n} \right ]=(4;6;4)\)

(Q) là mặt phẳng đi qua gốc tọa độ O(0;0;0), (Q) song song với AB và vuông góc với mặt phẳng (P) suy ra mặt phẳng (Q) nhận 

\(\overrightarrow {{n_{(Q)}}} = \frac{1}{2}\left[ {\overrightarrow {AB} ;\vec n} \right] = (2;3;2)\) làm VTPT.

Vậy phương trình mặt phẳng (Q) là: 

\(2x+3y+2z=0.\)

b. \(\overrightarrow{AB}=(-4;4;-2)\)

\(\Rightarrow AB=\sqrt{16+16+4}=6\)

Trung điểm AB là \(I(-2;-1;-2)\).

Mặt cầu (S) có tâm I, bán kính \(R=\frac{AB}{2}=3\) có phương trình là:

\((S):(x+2)^2+(y+1)^2+(z+2)^2=9\).

Bài tập 2: 

Cho mặt cầu 

\((S): x^2+y^2+z^2-2x+6y+4z-22=0\) 

và \((\alpha ):x+2y-2z-8=0\).

CRM: \((\alpha )\) cắt (S) theo một đường tròn. Xác định tâm, bán kính đường tròn đó.

Lời giải:

Nhận xét:
Tâm đường tròn giao tuyến của mặt cầu S(I;R) và \((\alpha )\) là hình chiếu của I trên \((\alpha )\) với \(r^2+d^2(I;(\alpha ))=R^2\).

\((S): (x-1)^2+(y+3)^2+(z+2)^2=36\)

Mặt cầu (S) có tâm I(1;-3;-2), bán kính R = 6.

\(d(I;(\alpha ))=\frac{\left | 1-6+4-8 \right |}{\sqrt{1^2+2^2+(-2)^2}}=\frac{9}{3}=3\) Vậy \((\alpha )\) cắt mặt cầu theo 1 đường tròn.

* Xác định tâm của H của đường tròn giao tuyến

Ta có H là hình chiếu của I trên \((\alpha )\).

Đường thẳng \(\Delta\) đi qua I và vuông góc với  \((\alpha )\), tức là nhận \(\vec{n_\alpha }=(1;2;-2)\) làm một VTCP có phương trình là:

\(\Delta \left\{\begin{matrix} x=1+t\\ y=-3+2t\\ z=-2-2t \end{matrix}\right.\)

\(H =\Delta \cap (\alpha )\)

\(H\in \Delta \Rightarrow H(1+t;-3+2t;-2-2t)\)

\(H\in (\alpha ) suy ra:

\(1+t+2(-3+2t)-2(-2-2t)-8=0\)

\(\Leftrightarrow 9t-9=0\Leftrightarrow t=1\)

Suy ra tọa độ H(2;-1;-4).

Bán kính đường trình giao tuyến: 

\(r^2=R^2-IH^2=36-9=27.\)

Vậy \(r=3\sqrt{3}.\)

Bài tập 3:

Cho đường thẳng \(d:\frac{x-12}{4}=\frac{y-9}{3}=\frac{z-1}{1}\) 

và \((P):3x+5y-z-2=0\)

a) Tìm tọa độ giao điểm A của d và (P).

b) Viết phương trình (Q) đi qua M₀(1;2;-1) và vuông góc với d.

c) Tìm tọa độ B' đối xứng với B(1;0;-1) qua (P).

Lời giải:

a) \(A=d\cap (P)\)

\(A\in d\left\{\begin{matrix} x=12+4t\\ y=9+3t\\ z=1+t \end{matrix}\right. \)

\(\Rightarrow A(12+4t;9+3t;1+t)\)

\(A\in (P)\) suy ra:

\(3(12+4t)+5(9+3t)-(1+t)-2=0\)

\(\Leftrightarrow 26t +78=0\Leftrightarrow t=-3\)

Vậy tọa độ là A(0;0;-2).

b) \((Q)\perp d\) nên (Q) nhận 

\(\vec{u_d}=(4;3;1)\) làm một VTPT.

Phương trình mặt phẳng (Q) là:

\((Q):4(x-1)+3(y-2)+1(z+1)=0\) 

Hay \(4x+3y+z-9=0.\)

c) Viết phương trình \(\Delta\) đi qua B và vuông góc (P)

\(\Delta\) \(\perp\) (P) nên \(\Delta\) nhận \(\vec{n_P}=(3;5;-1)\) làm một VTCP.

Phương trình tham số của \(\Delta: \)

\(\left\{\begin{matrix} x=1+3t\\ y=5t\\ z=-1-t \end{matrix}\right.\)

H là hình chiếu của B trên (P)

\(H=\Delta \cap (P)\)

\(H\in \Delta \Rightarrow H(1+3t;5t;-1-t)\)

\(H\in(P)\) suy ra:

\(3(1+3t)+25t+1+t-2=0\)

\(\Leftrightarrow 35t+2=0\)

\(\Leftrightarrow t=-\frac{2}{35}\)

\(H\left ( \frac{29}{35};-\frac{2}{7};-\frac{33}{35} \right )\)

H là trung điểm BB' nên: \(\left\{\begin{matrix} x_{B'}=2x_H-x_B=\frac{23}{35}\\ \\ y_{B'}=2y_H-y_B=-\frac{4}{7}\\ \\ z_{B'}=2z_H-z_B=\frac{2}{35} \end{matrix}\right.\)

Vậy tọa độ \(B' \left ( \frac{23}{35};-\frac{4}{7};\frac{2}{35} \right ).\)