Bài 20: Mạch dao động
Video bài giảng
1. Mạch dao động
-
Định nghĩa: Một cuộn cảm có độ tự cảm L mắc nối tiếp với một tụ điện có điện dung C thành một mạch điện kín gọi là mạch dao động.
-
Nếu điện trở của mạch rất nhỏ coi như bằng không thì mạch là một mạch dao động lí tưởng.
-
Muốn cho mạch dao động hoạt động thì ta tích điện cho tụ điện rồi cho nó phóng điện trong mạch. Tụ điện sẽ phóng điện qua lại nhiều lần, tạo ra một dòng điện xoay chiều trong mạch.
-
Người ta sử dụng điện áp xoay chiều được tạo ra giữa hai bản tụ điện bằng cách nối hai bản này với mạch ngoài.
2. Dao động điện từ tự do trong mạch dao động
a. Sự biến thiên điện tích và cường độ dòng điện trong một mạch dao động lí tưởng
-
Điện tích trên tụ điện biến thiên điều hòa theo thời gian:
\(q = Q_0\cos (\omega t + \varphi )\)
-
Cường độ dòng điện chạy trong mạch dao động biến thiên điều hòa theo thời gian:
Phương trình cường độ dòng điện:
\(\begin{array}{l}
(i = q' = - \omega {Q_0}.\sin (\omega t + \varphi )\\
\Rightarrow i = {I_0}.\cos (\omega t + \varphi + \frac{\pi }{2})
\end{array}\)
Với:
\(\omega = \frac{1}{\sqrt{LC}}\) và \(I_0 = \omega Q_0\)
-
Kết luận: Vậy, điện tích q của một bản tụ điện và cường độ dòng điện i trong mạch dao động biến thiên điều hoà theo thời gian; i lệch pha \(\frac{\pi }{2}\)so với q.
b. Định nghĩa dao động điện từ tự do
-
Sự biến thiên theo thời gian của điện tích q của một bản tụ điện và cường độ dòng điện i (hoặc cường độ điện trường \(\underset{E}{\rightarrow}\)và cảm ứng từ \(\underset{B}{\rightarrow}\) ) trong mạch dao động được gọi là dao động điện từ tự do.
c. Chu kì và tần số riêng của mạch dao động
-
Chu kì dao động riêng:
\(T = \frac{2 \pi }{\omega } = 2 \pi .\sqrt{LC}\)
-
Tần số dao động riêng :
\(f = \frac{1}{T} = \frac{1}{2\pi .\sqrt{LC}}\)
3. Năng lượng điện từ
-
Năng lượng điện trường:
\(\begin{array}{l}
{W_C} = \frac{1}{2}C{u^2}\\
= \frac{1}{2}CU_0^2.{\cos ^2}(\omega t + \varphi )
\end{array}\)
-
Năng lượng từ trường:
\(\begin{array}{l}
{W_L} = \frac{1}{2}L{i^2}\\
= \frac{1}{2}LI_0^2.{\sin ^2}(\omega t + \varphi )
\end{array}\)
-
Năng lượng điện từ:
\(W = W_C + W_L = \frac{1}{2}Cu^2 + \frac{1}{2}Li^2 = \frac{Q_{0}^{2}}{2C}\) (hằng số)
→ Tổng năng lượng điện trường và năng lượng từ trường của mạgh gọi là năng lượng điện từ
-
\(W = W_{C\ max}\ (W_L = 0)\)
-
\(W = W_{L\ max}\ (W_C = 0)\)
Bài 1:
Cho mạch LC lý tưởng gồm L = 4 mH; C = 9 nF; \(U_0\) = 12 V
a) Tìm \(\omega\), T, f, I0, Q0, W?
b) Viết biểu thức q biết tại t = 0, \(q = \frac{Q_0}{2}\) và đang tăng? Suy ra biểu thức u và i?
c) Tìm \(\frac{W_C}{W_L}\) khi i = 3 mA và khi u = 4 V?
d) Trong 1 chu kỳ, tìm thời gian để độ lớn cường độ dòng điện i không vượt quá \(9\sqrt{3}\) mA?
Hướng dẫn giải:
L = 4 mH = \(4.10^{-3}\) H
C = 9 nF = \(9.10^{-9}\) F
\(U_0\) = 12 V
a)
\(\begin{array}{l}
\bullet \omega = \frac{1}{{\sqrt {LC} }}\\
= \frac{1}{{\sqrt {{{4.10}^{ - 3}}{{.9.10}^{ - 9}}} }} = \frac{{{{10}^6}}}{6}\;(rad/s)\\
\bullet T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{{{10}^6}}}{6}}}\\
= 12\pi {.10^{ - 6}}\;(s)\\
\bullet f = \frac{1}{T} = \frac{1}{{12\pi {{.10}^{ - 6}}}}\\
= \frac{{{{10}^6}}}{{12\pi }}\;(Hz)\\
{I_0} = \omega {Q_0}\\
{Q_0} = C{U_0} = {9.10^{ - 9}}.12\\
\Leftrightarrow {Q_0} = {108.10^{ - 9}}\;(C)\\
\Rightarrow {I_0} = \omega {Q_0} = \frac{{{{10}^6}}}{6}{.108.10^{ - 9}}\\
= {18.10^{ - 3}}\;(A) = 18\;(mA)\\
\bullet W = \frac{1}{2}CU_0^2 = \frac{1}{2}{.9.10^{ - 9}}{.12^2}\\
\Rightarrow W = {648.10^{ - 9}}\;(J)
\end{array}\)
b) \(q = Q_0 \cos (\omega t + \varphi )\)
\(\begin{array}{l}
t = 0\\
q = \frac{{{Q_0}}}{2}\\
\Rightarrow \frac{{{Q_0}}}{2} = {Q_0}\cos \varphi \\
\Rightarrow \cos \varphi = \frac{1}{2}\\
\Rightarrow \varphi = \pm \frac{\pi }{3}\\
\Rightarrow \varphi = \frac{\pi }{3}
\end{array}\)
Vậy \(q = 108.10^{-9}.\cos (\frac{10^6}{6} t - \frac{\pi }{3}) \ (C)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{u = 12\cos \left( {\frac{{{{10}^6}}}{6}t - \frac{\pi }{3}} \right)\;(V)}\\
{i = 18\cos \left( {\frac{{{{10}^6}}}{6}t - \frac{\pi }{3} + \frac{\pi }{2}} \right)\;(mA)}
\end{array}} \right.\)
c)
\(\begin{array}{l}
\cdot \;\left\{ {\begin{array}{*{20}{c}}
{\frac{{{W_C}}}{{{W_L}}} = \;?\;\;\;}\\
{i = 3\;mA}
\end{array}} \right.\\
\frac{{{W_C}}}{{{W_L}}} = \frac{{W - {W_L}}}{{{W_L}}}\\
= \frac{W}{{{W_L}}} - 1 = \frac{{\frac{1}{2}LI_0^2}}{{\frac{1}{2}L{i^2}}} - 1\\
\Rightarrow \frac{{{W_C}}}{{{W_L}}} = {\left( {\frac{{{I_0}}}{i}} \right)^2} - 1 = 35
\end{array}\)
\(\begin{array}{l}
\cdot \;\left\{ {\begin{array}{*{20}{c}}
{\frac{{{W_C}}}{{{W_L}}} = \;?\;\;}\\
{u = 4\;V}
\end{array}} \right.\\
\Rightarrow \frac{{{W_C}}}{{{W_L}}} = \frac{{{W_C}}}{{W - {W_C}}}\\
= \frac{{\frac{1}{2}C{u^2}}}{{\frac{1}{2}CU_0^2 - {u^2}}} = \frac{{{u^2}}}{{U_0^2 - {u^2}}}\\
\Rightarrow \frac{{{W_C}}}{{{W_L}}} = \frac{1}{8}
\end{array}\)
d)
\(\begin{array}{l}
Trong\;1T:\\
\left| i \right| \le 9\sqrt 3 \;mA = \frac{{{I_0}\sqrt 3 }}{2}\\
\Rightarrow \Delta t = \;?
\end{array}\)
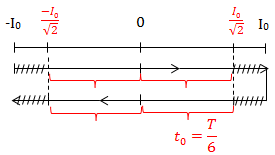
\(\begin{array}{l}
\Rightarrow \Delta t = 4{t_0} = 4\frac{T}{6}\\
= \frac{2}{3}.12\pi {.10^{ - 6}}\\
= 8\pi {.10^{ - 6}}\;(s)
\end{array}\)
Bài 2:
Trong một mạch dao động lý tưởng. Lúc cường độ dòng điện trong mạch bằng không, thì hiệu điện thế trên tụ bằng 10V. Xác định hiệu điện thế trên tụ điện vào lúc năng lượng từ trường trong cuộn dây gấp ba lần năng lượng điện trường trong tụ điện?
Hướng dẫn giải:
-
Ta có :
\({U_{0}} = 10{\rm{ }}V\)
-
Áp dụng định luật bảo toàn năng lượng ta có:
\(\begin{array}{l}
\frac{{C{u^2}}}{2} + \frac{{L{i^2}}}{2} = \frac{{CU_0^2}}{2}\\
\Rightarrow \frac{{C{u^2}}}{2} + 3\frac{{C{u^2}}}{2} = \frac{{CU_0^2}}{2}\\
\Rightarrow {u^2} = \frac{{U_0^2}}{4}\\
\Rightarrow u = \sqrt {\frac{{{{10}^2}}}{4}} = 5V
\end{array}\)
1. Mạch dao động
-
Định nghĩa: Một cuộn cảm có độ tự cảm L mắc nối tiếp với một tụ điện có điện dung C thành một mạch điện kín gọi là mạch dao động.
-
Nếu điện trở của mạch rất nhỏ coi như bằng không thì mạch là một mạch dao động lí tưởng.
-
Muốn cho mạch dao động hoạt động thì ta tích điện cho tụ điện rồi cho nó phóng điện trong mạch. Tụ điện sẽ phóng điện qua lại nhiều lần, tạo ra một dòng điện xoay chiều trong mạch.
-
Người ta sử dụng điện áp xoay chiều được tạo ra giữa hai bản tụ điện bằng cách nối hai bản này với mạch ngoài.
2. Dao động điện từ tự do trong mạch dao động
a. Sự biến thiên điện tích và cường độ dòng điện trong một mạch dao động lí tưởng
-
Điện tích trên tụ điện biến thiên điều hòa theo thời gian:
\(q = Q_0\cos (\omega t + \varphi )\)
-
Cường độ dòng điện chạy trong mạch dao động biến thiên điều hòa theo thời gian:
Phương trình cường độ dòng điện:
\(\begin{array}{l}
(i = q' = - \omega {Q_0}.\sin (\omega t + \varphi )\\
\Rightarrow i = {I_0}.\cos (\omega t + \varphi + \frac{\pi }{2})
\end{array}\)
Với:
\(\omega = \frac{1}{\sqrt{LC}}\) và \(I_0 = \omega Q_0\)
-
Kết luận: Vậy, điện tích q của một bản tụ điện và cường độ dòng điện i trong mạch dao động biến thiên điều hoà theo thời gian; i lệch pha \(\frac{\pi }{2}\)so với q.
b. Định nghĩa dao động điện từ tự do
-
Sự biến thiên theo thời gian của điện tích q của một bản tụ điện và cường độ dòng điện i (hoặc cường độ điện trường \(\underset{E}{\rightarrow}\)và cảm ứng từ \(\underset{B}{\rightarrow}\) ) trong mạch dao động được gọi là dao động điện từ tự do.
c. Chu kì và tần số riêng của mạch dao động
-
Chu kì dao động riêng:
\(T = \frac{2 \pi }{\omega } = 2 \pi .\sqrt{LC}\)
-
Tần số dao động riêng :
\(f = \frac{1}{T} = \frac{1}{2\pi .\sqrt{LC}}\)
3. Năng lượng điện từ
-
Năng lượng điện trường:
\(\begin{array}{l}
{W_C} = \frac{1}{2}C{u^2}\\
= \frac{1}{2}CU_0^2.{\cos ^2}(\omega t + \varphi )
\end{array}\)
-
Năng lượng từ trường:
\(\begin{array}{l}
{W_L} = \frac{1}{2}L{i^2}\\
= \frac{1}{2}LI_0^2.{\sin ^2}(\omega t + \varphi )
\end{array}\)
-
Năng lượng điện từ:
\(W = W_C + W_L = \frac{1}{2}Cu^2 + \frac{1}{2}Li^2 = \frac{Q_{0}^{2}}{2C}\) (hằng số)
→ Tổng năng lượng điện trường và năng lượng từ trường của mạgh gọi là năng lượng điện từ
-
\(W = W_{C\ max}\ (W_L = 0)\)
-
\(W = W_{L\ max}\ (W_C = 0)\)
Bài 1:
Cho mạch LC lý tưởng gồm L = 4 mH; C = 9 nF; \(U_0\) = 12 V
a) Tìm \(\omega\), T, f, I0, Q0, W?
b) Viết biểu thức q biết tại t = 0, \(q = \frac{Q_0}{2}\) và đang tăng? Suy ra biểu thức u và i?
c) Tìm \(\frac{W_C}{W_L}\) khi i = 3 mA và khi u = 4 V?
d) Trong 1 chu kỳ, tìm thời gian để độ lớn cường độ dòng điện i không vượt quá \(9\sqrt{3}\) mA?
Hướng dẫn giải:
L = 4 mH = \(4.10^{-3}\) H
C = 9 nF = \(9.10^{-9}\) F
\(U_0\) = 12 V
a)
\(\begin{array}{l}
\bullet \omega = \frac{1}{{\sqrt {LC} }}\\
= \frac{1}{{\sqrt {{{4.10}^{ - 3}}{{.9.10}^{ - 9}}} }} = \frac{{{{10}^6}}}{6}\;(rad/s)\\
\bullet T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{{{10}^6}}}{6}}}\\
= 12\pi {.10^{ - 6}}\;(s)\\
\bullet f = \frac{1}{T} = \frac{1}{{12\pi {{.10}^{ - 6}}}}\\
= \frac{{{{10}^6}}}{{12\pi }}\;(Hz)\\
{I_0} = \omega {Q_0}\\
{Q_0} = C{U_0} = {9.10^{ - 9}}.12\\
\Leftrightarrow {Q_0} = {108.10^{ - 9}}\;(C)\\
\Rightarrow {I_0} = \omega {Q_0} = \frac{{{{10}^6}}}{6}{.108.10^{ - 9}}\\
= {18.10^{ - 3}}\;(A) = 18\;(mA)\\
\bullet W = \frac{1}{2}CU_0^2 = \frac{1}{2}{.9.10^{ - 9}}{.12^2}\\
\Rightarrow W = {648.10^{ - 9}}\;(J)
\end{array}\)
b) \(q = Q_0 \cos (\omega t + \varphi )\)
\(\begin{array}{l}
t = 0\\
q = \frac{{{Q_0}}}{2}\\
\Rightarrow \frac{{{Q_0}}}{2} = {Q_0}\cos \varphi \\
\Rightarrow \cos \varphi = \frac{1}{2}\\
\Rightarrow \varphi = \pm \frac{\pi }{3}\\
\Rightarrow \varphi = \frac{\pi }{3}
\end{array}\)
Vậy \(q = 108.10^{-9}.\cos (\frac{10^6}{6} t - \frac{\pi }{3}) \ (C)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{u = 12\cos \left( {\frac{{{{10}^6}}}{6}t - \frac{\pi }{3}} \right)\;(V)}\\
{i = 18\cos \left( {\frac{{{{10}^6}}}{6}t - \frac{\pi }{3} + \frac{\pi }{2}} \right)\;(mA)}
\end{array}} \right.\)
c)
\(\begin{array}{l}
\cdot \;\left\{ {\begin{array}{*{20}{c}}
{\frac{{{W_C}}}{{{W_L}}} = \;?\;\;\;}\\
{i = 3\;mA}
\end{array}} \right.\\
\frac{{{W_C}}}{{{W_L}}} = \frac{{W - {W_L}}}{{{W_L}}}\\
= \frac{W}{{{W_L}}} - 1 = \frac{{\frac{1}{2}LI_0^2}}{{\frac{1}{2}L{i^2}}} - 1\\
\Rightarrow \frac{{{W_C}}}{{{W_L}}} = {\left( {\frac{{{I_0}}}{i}} \right)^2} - 1 = 35
\end{array}\)
\(\begin{array}{l}
\cdot \;\left\{ {\begin{array}{*{20}{c}}
{\frac{{{W_C}}}{{{W_L}}} = \;?\;\;}\\
{u = 4\;V}
\end{array}} \right.\\
\Rightarrow \frac{{{W_C}}}{{{W_L}}} = \frac{{{W_C}}}{{W - {W_C}}}\\
= \frac{{\frac{1}{2}C{u^2}}}{{\frac{1}{2}CU_0^2 - {u^2}}} = \frac{{{u^2}}}{{U_0^2 - {u^2}}}\\
\Rightarrow \frac{{{W_C}}}{{{W_L}}} = \frac{1}{8}
\end{array}\)
d)
\(\begin{array}{l}
Trong\;1T:\\
\left| i \right| \le 9\sqrt 3 \;mA = \frac{{{I_0}\sqrt 3 }}{2}\\
\Rightarrow \Delta t = \;?
\end{array}\)

\(\begin{array}{l}
\Rightarrow \Delta t = 4{t_0} = 4\frac{T}{6}\\
= \frac{2}{3}.12\pi {.10^{ - 6}}\\
= 8\pi {.10^{ - 6}}\;(s)
\end{array}\)
Bài 2:
Trong một mạch dao động lý tưởng. Lúc cường độ dòng điện trong mạch bằng không, thì hiệu điện thế trên tụ bằng 10V. Xác định hiệu điện thế trên tụ điện vào lúc năng lượng từ trường trong cuộn dây gấp ba lần năng lượng điện trường trong tụ điện?
Hướng dẫn giải:
-
Ta có :
\({U_{0}} = 10{\rm{ }}V\)
-
Áp dụng định luật bảo toàn năng lượng ta có:
\(\begin{array}{l}
\frac{{C{u^2}}}{2} + \frac{{L{i^2}}}{2} = \frac{{CU_0^2}}{2}\\
\Rightarrow \frac{{C{u^2}}}{2} + 3\frac{{C{u^2}}}{2} = \frac{{CU_0^2}}{2}\\
\Rightarrow {u^2} = \frac{{U_0^2}}{4}\\
\Rightarrow u = \sqrt {\frac{{{{10}^2}}}{4}} = 5V
\end{array}\)