Bài 10: Đặc trưng Vật lý của âm
Video bài giảng
1. Âm. Nguồn âm
1.1. Âm là gì ?
-
Sóng âm (âm) là những sóng cơ lan truyền trong các môi trường rắn, lỏng, khí.
1.2. Nguồn âm là gì?
-
Nguồn âm là những vật dao động phát ra âm.
-
Tần số âm phát ra bằng tần số dao động của nguồn.
1.3. Âm nghe được, hạ âm, siêu âm
Ví dụ :
Những con vật có thể phát và cảm nhận sóng hạ âm, siêu âm
1.4. Sự truyền âm
-
Môi trường truyền âm:
-
Âm truyền được trong các môi trường rắn, lỏng, khí; không truyền được trong chân không.
-
Âm hầu như không truyền qua được các chất xốp như bông, len…\(\rightarrow\)gọi là chất cách âm.
-
-
Tốc độ truyền âm:
-
Trong mỗi môi trường, âm truyền với một tốc độ xác định, hữu hạn.
-
-
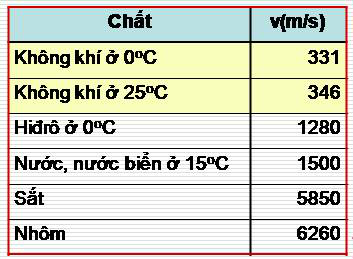
Ví dụ: Tốc độ truyền âm trong 1 số chất:
2. Những đặc trưng vật lý của âm
2.1. Tần số âm
-
Tần số âm là một trong những đặc trưng vật lí quan trọng nhất của âm.
2.2. Cường độ âm và mức cường độ âm
-
Cường độ âm:
-
Cường độ âm là năng lượng của sóng âm truyền qua một đơn vị diện tích đặt vuông góc với phương truyền sóng trong một đơn vị thời gian.
-
Kí hiệu: I
-
Đơn vị: W/m2 (oát trên mét vuông).
-
-
-
Mức cường độ âm:
-
Công thức: L(B) = \(\log\frac{I}{I_0}\)
-
Đơn vị: B (ben)
-
Nếu dùng đơn vị dB (đêxiben): 1B=10dB
-
hay L(dB) = 10lg(\(\frac{I}{I_0}\))
-
Một số mức cường độ âm đáng chú ý:
-
0 dB: Ngưỡng nghe
-
30 dB: Tiếng thì thầm
-
40 dB: Tiếng nói chuyện bình thường
-
60 dB: Tiếng ồn áo trong cửa hàng lớn
-
90 dB: Tiếng ồn ngoài phố
-
120 dB: Tiếng sét lớn, máy bay lúc cất cánh
-
130 dB: Ngưỡng đau
-
2.3. Âm cơ bản và họa âm.
-
Nếu dây rung với một bó sóng thì dây phát ra âm có tần số thấp nhất (tần số fmin đã biết trong bài Sóng dừng). Ta hãy gọi tần số này là tần số fo và gọi là âm cơ bản (còn gọi là họa âm thứ 1).
-
Khảo sát thực nghiệm cho thấy dây này còn phát ra các âm có tần số 2fo, 3fo, 4fo .... gọi là họa âm thứ 2, họa âm thứ 3, họa âm thứ 4, ... Các họa âm có biên độ khác nhau khiến đồ thị dao động âm của các nhạc cụ khi phát ra cùng một nốt nhạc cũng khác nhau. Sự khác nhau này phân biệt được bởi âm sắc của chúng.
-
Đặc trưng vật lí thứ ba của âm là đồ thị dao động của âm đó.
Bài 1:
Cường độ âm tại một điểm trong môi trừơng truyền âm là \(10^{-5}W/m^2\). biết cường độ âm chuẩn là \(I_0=10^{-12} W/m^2\) . Mức cường độ âm tại điểm đó là bao nhiêu?
Hướng dẫn giải :
\(L(dB)=10log\frac{I}{I_0}=10log\frac{10^{-5}}{10^{-12}}=70(dB)\)
Bài 2:
Gọi \(I_0\) là cường độ âm chuẩn , nếu cho mức cường độ âm là 1(dB) , tính cường độ âm ?
Hướng dẫn giải :
\(\begin{array}{l} lg\frac{I}{{{I_0}}} = {10^{ - 1}} = 0,1\\ \to I = {10^{0,1}}{I_0} = 1,26{I_0} \end{array}\)
Bài 3:
Một nguồn âm là nguồn điểm phát âm đẳng hướng trong không gian. Giả sử không có sự hấp thụ và phản xạ âm. Tại 1 điểm cách nguồn âm 10m thì mức cường độ âm là 80dB, tại điểm cách nguồn âm 1m thì mức cường độ âm có giá trị bao nhiêu ?
Hướng dẫn giải :
\(\begin{array}{l} \frac{{{I_1}}}{{{I_2}}} = {(\frac{{{R_2}}}{{{R_1}}})^2} = \frac{1}{{100}}\\ \to {I_2} = 100{I_1}\\ {L_1} = 10lg\frac{{{I_1}}}{{{I_0}}}(dB);\\ {L_2} = 10lg\frac{{{I_2}}}{{{I_0}}}(dB) = 10lg\frac{{100{I_1}}}{{{I_0}}}(dB)\\ \to {L_2} = 10(2 + log\frac{I}{{{I_0}}}) = 20 + {L_2} = 100(dB) \end{array}\)
1. Âm. Nguồn âm
1.1. Âm là gì ?
-
Sóng âm (âm) là những sóng cơ lan truyền trong các môi trường rắn, lỏng, khí.
1.2. Nguồn âm là gì?
-
Nguồn âm là những vật dao động phát ra âm.
-
Tần số âm phát ra bằng tần số dao động của nguồn.
1.3. Âm nghe được, hạ âm, siêu âm
Ví dụ :
Những con vật có thể phát và cảm nhận sóng hạ âm, siêu âm
1.4. Sự truyền âm
-
Môi trường truyền âm:
-
Âm truyền được trong các môi trường rắn, lỏng, khí; không truyền được trong chân không.
-
Âm hầu như không truyền qua được các chất xốp như bông, len…\(\rightarrow\)gọi là chất cách âm.
-
-
Tốc độ truyền âm:
-
Trong mỗi môi trường, âm truyền với một tốc độ xác định, hữu hạn.
-
-
Ví dụ: Tốc độ truyền âm trong 1 số chất:
2. Những đặc trưng vật lý của âm
2.1. Tần số âm
-
Tần số âm là một trong những đặc trưng vật lí quan trọng nhất của âm.
2.2. Cường độ âm và mức cường độ âm
-
Cường độ âm:
-
Cường độ âm là năng lượng của sóng âm truyền qua một đơn vị diện tích đặt vuông góc với phương truyền sóng trong một đơn vị thời gian.
-
Kí hiệu: I
-
Đơn vị: W/m2 (oát trên mét vuông).
-
-
-
Mức cường độ âm:
-
Công thức: L(B) = \(\log\frac{I}{I_0}\)
-
Đơn vị: B (ben)
-
Nếu dùng đơn vị dB (đêxiben): 1B=10dB
-
hay L(dB) = 10lg(\(\frac{I}{I_0}\))
-
Một số mức cường độ âm đáng chú ý:
-
0 dB: Ngưỡng nghe
-
30 dB: Tiếng thì thầm
-
40 dB: Tiếng nói chuyện bình thường
-
60 dB: Tiếng ồn áo trong cửa hàng lớn
-
90 dB: Tiếng ồn ngoài phố
-
120 dB: Tiếng sét lớn, máy bay lúc cất cánh
-
130 dB: Ngưỡng đau
-
2.3. Âm cơ bản và họa âm.
-
Nếu dây rung với một bó sóng thì dây phát ra âm có tần số thấp nhất (tần số fmin đã biết trong bài Sóng dừng). Ta hãy gọi tần số này là tần số fo và gọi là âm cơ bản (còn gọi là họa âm thứ 1).
-
Khảo sát thực nghiệm cho thấy dây này còn phát ra các âm có tần số 2fo, 3fo, 4fo .... gọi là họa âm thứ 2, họa âm thứ 3, họa âm thứ 4, ... Các họa âm có biên độ khác nhau khiến đồ thị dao động âm của các nhạc cụ khi phát ra cùng một nốt nhạc cũng khác nhau. Sự khác nhau này phân biệt được bởi âm sắc của chúng.
-
Đặc trưng vật lí thứ ba của âm là đồ thị dao động của âm đó.
Bài 1:
Cường độ âm tại một điểm trong môi trừơng truyền âm là \(10^{-5}W/m^2\). biết cường độ âm chuẩn là \(I_0=10^{-12} W/m^2\) . Mức cường độ âm tại điểm đó là bao nhiêu?
Hướng dẫn giải :
\(L(dB)=10log\frac{I}{I_0}=10log\frac{10^{-5}}{10^{-12}}=70(dB)\)
Bài 2:
Gọi \(I_0\) là cường độ âm chuẩn , nếu cho mức cường độ âm là 1(dB) , tính cường độ âm ?
Hướng dẫn giải :
\(\begin{array}{l} lg\frac{I}{{{I_0}}} = {10^{ - 1}} = 0,1\\ \to I = {10^{0,1}}{I_0} = 1,26{I_0} \end{array}\)
Bài 3:
Một nguồn âm là nguồn điểm phát âm đẳng hướng trong không gian. Giả sử không có sự hấp thụ và phản xạ âm. Tại 1 điểm cách nguồn âm 10m thì mức cường độ âm là 80dB, tại điểm cách nguồn âm 1m thì mức cường độ âm có giá trị bao nhiêu ?
Hướng dẫn giải :
\(\begin{array}{l} \frac{{{I_1}}}{{{I_2}}} = {(\frac{{{R_2}}}{{{R_1}}})^2} = \frac{1}{{100}}\\ \to {I_2} = 100{I_1}\\ {L_1} = 10lg\frac{{{I_1}}}{{{I_0}}}(dB);\\ {L_2} = 10lg\frac{{{I_2}}}{{{I_0}}}(dB) = 10lg\frac{{100{I_1}}}{{{I_0}}}(dB)\\ \to {L_2} = 10(2 + log\frac{I}{{{I_0}}}) = 20 + {L_2} = 100(dB) \end{array}\)
.PNG)
.PNG)