Bài 9: Sóng dừng
Video bài giảng
1. Sự phản xạ của sóng
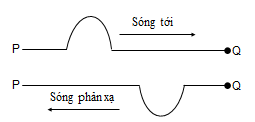
1.1. Phản xạ của sóng trên vật cản cố định
-
Khi phản xạ trên vật cản cố định, sóng phản xạ luôn luôn ngược pha với sóng tới ở điểm phản xạ.
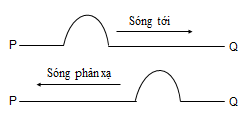
1.2. Phản xạ của sóng trên vật cản tự do.
-
Khi phản xạ trên vật cản tự do, sóng phản xạ luôn luôn cùng pha với sóng tới ở điểm phản xạ.
2. Sóng dừng
2.1. Định nghĩa sóng dừng
-
Sóng truyền trên sợi dây trong trường hợp xuất hiện các nút và các bụng gọi là sóng dừng.
-
Chú ý : Các vị trí bụng là cực đại của biên độ, các vị trí nút là cực tiểu của biên độ.
2.2. Sóng dừng trên sợi dây có hai đầu cố định.

-
Đối với sợi dây có hai đầu cố định:
-
Số bó sóng: k
-
Số nút sóng: k + 1
-
Số bụng sóng: k
-
\(\Rightarrow \lambda = \frac{2\ell }{k} \Rightarrow \lambda _{max } = 2 \ell \ (Khi \ k = 1)\)
-
Điều kiện để có sóng dừng trên sợi dây có hai đầu cố định :
\(l = k\frac{\lambda }{2}\)
-
Điều kiện để có sóng dừng trên một sợi dây có hai đầu cố định là chiều dài của sợi dây phải bằng một số nguyên lần nữa bước sóng.
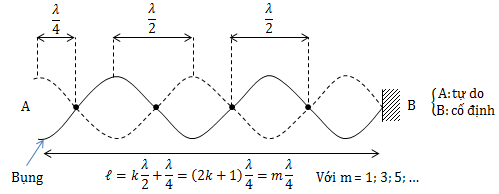
2.3. Sóng dừng trên một sợi dây có một đầu cố định, một đầu tự do.
-
Đối với sợi dây có một đầu cố định, một đầu tự do
-
Số bó sóng: k
-
Số nút sóng: k + 1
-
Số bụng sóng: k + 1
-
⇒ \(\lambda = \frac{4\ell}{2k + 1} \Rightarrow \lambda _{max} = 4 \ell \ (Khi \ k = 0)\)
-
Điều kiện có sóng dừng:
\(l=(2k+1)\frac{\lambda }{2}\)
-
Điều kiện để có sóng dừng trên một sợi dây có một đầu cố định, một đầu tự do là chiều dài của sợi dây phải bằng một số lẻ lần \(\frac{\lambda }{4}\)
Bài 1
Một sợi dây AB có chiều dài 13cm, đầu A gắn vào một nhánh âm thoa còn đầu B dao động tự do. Cho âm thoa dao động theo phương ngang với tần số \(f\) = 20Hz, ta thấy trên dây có sóng dừng với 7 nút sóng (kể cả A). Tốc độ truyền sóng trên dây bằng bao nhiêu?
Hướng dẫn giải:
-
Vì sóng dừng xảy ra với một đầu là nút và một đầu tự do nên
\(\begin{array}{l} l = (2k + 1)\frac{\lambda }{4}\\ \Leftrightarrow 13 = (2.(7 - 1) + 1)\frac{\lambda }{4}\\ \to \lambda = 4(cm)\\ \to v = \lambda .f = 80(\frac{{cm}}{s}) \end{array}\)
Bài 2:
Trên sợi dây dài 2 m đang có sóng dừng với tần số 100 Hz. Người ta thấy ngoài 2 đầu dây cố định còn có 3 điểm khác luôn đứng yên. Tìm tốc độ truyền sóng?
Hướng dẫn giải:
-
Ta có: \(\ell = 2 \ m; \ f = 100\ Hz\)
-
Trên dây có 5 nút cùng với gỉa thiết hai đầu cố định ⇒ k = 4
\(\begin{array}{l} \ell = k\frac{\lambda }{2}\\ \Rightarrow \lambda = \frac{{2\ell }}{k} = \frac{{2.2}}{4} = 1\;(m) \end{array}\)
\(\rightarrow v = \lambda .f = 100\ m/s\)
Bài 3:
Sợi dây AB dài 1 m, đầu A cố định, đầu B dao động với tần số thay đổi được và được xem là nút sóng. Ban đầu trên dây có sóng dừng, nếu tăng tần số thêm 30 Hz thì số nút trên dây tăng thêm 5 nút. Tìm tốc độ truyền sóng?
Hướng dẫn giải:
-
Ta có: \(\ell = 1\ m\)
-
Ban đầu: \(\ell = k\frac{\lambda }{2} = k = \frac{v}{2f}\)
\(\Rightarrow f = k\frac{v}{2 \ell } \ (1)\)
-
Nếu f + 30 và trên dây tăng 5 nút (⇒ tăng 5 bó sóng)
\(\Rightarrow f + 30 =(k + 5) \frac{v}{2 \ell }\)
\(\Leftrightarrow 30 = 5 \frac{v}{2 \ell }\)
-
Từ (1): \(f = k\frac{v}{2 \ell}\)
\(\begin{array}{l} \Rightarrow 30 = 5\frac{v}{{2\ell }}\\ \Rightarrow v = \frac{{60.1}}{{12}}\;m/s = {\rm{ }}5m/s \end{array}\)
1. Sự phản xạ của sóng
1.1. Phản xạ của sóng trên vật cản cố định
-
Khi phản xạ trên vật cản cố định, sóng phản xạ luôn luôn ngược pha với sóng tới ở điểm phản xạ.
1.2. Phản xạ của sóng trên vật cản tự do.
-
Khi phản xạ trên vật cản tự do, sóng phản xạ luôn luôn cùng pha với sóng tới ở điểm phản xạ.
2. Sóng dừng
2.1. Định nghĩa sóng dừng
-
Sóng truyền trên sợi dây trong trường hợp xuất hiện các nút và các bụng gọi là sóng dừng.
-
Chú ý : Các vị trí bụng là cực đại của biên độ, các vị trí nút là cực tiểu của biên độ.
2.2. Sóng dừng trên sợi dây có hai đầu cố định.

-
Đối với sợi dây có hai đầu cố định:
-
Số bó sóng: k
-
Số nút sóng: k + 1
-
Số bụng sóng: k
-
\(\Rightarrow \lambda = \frac{2\ell }{k} \Rightarrow \lambda _{max } = 2 \ell \ (Khi \ k = 1)\)
-
Điều kiện để có sóng dừng trên sợi dây có hai đầu cố định :
\(l = k\frac{\lambda }{2}\)
-
Điều kiện để có sóng dừng trên một sợi dây có hai đầu cố định là chiều dài của sợi dây phải bằng một số nguyên lần nữa bước sóng.
2.3. Sóng dừng trên một sợi dây có một đầu cố định, một đầu tự do.

-
Đối với sợi dây có một đầu cố định, một đầu tự do
-
Số bó sóng: k
-
Số nút sóng: k + 1
-
Số bụng sóng: k + 1
-
⇒ \(\lambda = \frac{4\ell}{2k + 1} \Rightarrow \lambda _{max} = 4 \ell \ (Khi \ k = 0)\)
-
Điều kiện có sóng dừng:
\(l=(2k+1)\frac{\lambda }{2}\)
-
Điều kiện để có sóng dừng trên một sợi dây có một đầu cố định, một đầu tự do là chiều dài của sợi dây phải bằng một số lẻ lần \(\frac{\lambda }{4}\)
Bài 1
Một sợi dây AB có chiều dài 13cm, đầu A gắn vào một nhánh âm thoa còn đầu B dao động tự do. Cho âm thoa dao động theo phương ngang với tần số \(f\) = 20Hz, ta thấy trên dây có sóng dừng với 7 nút sóng (kể cả A). Tốc độ truyền sóng trên dây bằng bao nhiêu?
Hướng dẫn giải:
-
Vì sóng dừng xảy ra với một đầu là nút và một đầu tự do nên
\(\begin{array}{l} l = (2k + 1)\frac{\lambda }{4}\\ \Leftrightarrow 13 = (2.(7 - 1) + 1)\frac{\lambda }{4}\\ \to \lambda = 4(cm)\\ \to v = \lambda .f = 80(\frac{{cm}}{s}) \end{array}\)
Bài 2:
Trên sợi dây dài 2 m đang có sóng dừng với tần số 100 Hz. Người ta thấy ngoài 2 đầu dây cố định còn có 3 điểm khác luôn đứng yên. Tìm tốc độ truyền sóng?
Hướng dẫn giải:
-
Ta có: \(\ell = 2 \ m; \ f = 100\ Hz\)
-
Trên dây có 5 nút cùng với gỉa thiết hai đầu cố định ⇒ k = 4
\(\begin{array}{l} \ell = k\frac{\lambda }{2}\\ \Rightarrow \lambda = \frac{{2\ell }}{k} = \frac{{2.2}}{4} = 1\;(m) \end{array}\)
\(\rightarrow v = \lambda .f = 100\ m/s\)
Bài 3:
Sợi dây AB dài 1 m, đầu A cố định, đầu B dao động với tần số thay đổi được và được xem là nút sóng. Ban đầu trên dây có sóng dừng, nếu tăng tần số thêm 30 Hz thì số nút trên dây tăng thêm 5 nút. Tìm tốc độ truyền sóng?
Hướng dẫn giải:
-
Ta có: \(\ell = 1\ m\)
-
Ban đầu: \(\ell = k\frac{\lambda }{2} = k = \frac{v}{2f}\)
\(\Rightarrow f = k\frac{v}{2 \ell } \ (1)\)
-
Nếu f + 30 và trên dây tăng 5 nút (⇒ tăng 5 bó sóng)
\(\Rightarrow f + 30 =(k + 5) \frac{v}{2 \ell }\)
\(\Leftrightarrow 30 = 5 \frac{v}{2 \ell }\)
-
Từ (1): \(f = k\frac{v}{2 \ell}\)
\(\begin{array}{l} \Rightarrow 30 = 5\frac{v}{{2\ell }}\\ \Rightarrow v = \frac{{60.1}}{{12}}\;m/s = {\rm{ }}5m/s \end{array}\)