Bài 9: Định luật Ôm đối với toàn mạch
1. Thí nghiệm
-
Toàn mạch là một mạch điện kín gồm: Nguồn điện (E,r) nối với mạch ngoài là các vật dẫn có điện trở tương đương R
-
Mắc mạch điện như hình vẽ:
Thiết lập định luật Ôm cho toàn mạch
-
Nguồn điện thực hiện 1 công \( A = EIt\).
-
Nhiệt lượng tỏa ra ở điện trở ngoài và điện trở trong của nguồn điện:
\(Q = R{I^2}t + r{I^2}t.\)
-
Theo Định luật bảo toàn và chuyển hóa năng lượng:
\(Q= A\) hay \(R{I^2}.t + {\rm{ }}r{I^2}.t = EIt\)
\(\begin{array}{l}
\Rightarrow E = RI + rI = I(R + r)\\
\Rightarrow I = \frac{E}{{R + r}}
\end{array}\)
-
Dùng thí nghiệm chứng minh để thiết lập biểu thức định luật Ôm cho toàn mạch
.PNG)
\({U_{AB}} = E - Ir\)
2. Định luật Ôm đối với toàn mạch
2.1. Biểu thức:
\({\mathop{\rm I}\nolimits} = \frac{E}{{{R_N} + r}}\) (1)
2.2. Phát biểu:
-
Cường độ dòng điện chạy trong mạch điện kín tỉ lệ thuận với suất điện động của nguồn điện và tỉ lệ nghịch với điện trở toàn phần của mạch đó.
-
Lưu ý:
\(\begin{array}{l}
{\rm{I}} = \frac{E}{{{R_N} + r}}\\
\Leftrightarrow E = {\rm{I}}({R_N} + r)\\
\Rightarrow E = {{\rm{U}}_N} + Ir
\end{array}\)
\(E = {U_N}\) Khi: r = 0 hoặc mạch hở (I = 0)
3. Nhận xét
3.1. Hiện tượng đoản mạch
-
Là hiện tượng nối tắt 2 cực của nguồn bằng dây dẫn có điện trở rất nhỏ.
-
Cường độ dòng điện trong mạch kín đạt giá trị lớn nhất khi \({R_N} = 0\) . Khi đó ta nói rằng nguồn điện bị đoản mạch.
\(I = \frac{E}{r}\) (2)
-
Khi đó: \(R \approx 0\) và \({I_{m{\rm{ax}}}} = \frac{E}{r}\)
-
Tác hại của hiện tượng đoản mạch là gây lên cháy chập mạch điện, đó chính là một trong những nguyên nhân dẫn tới các vụ cháy .
3.2. Định luật Ôm đối với toàn mạch và định luật bảo toàn và chuyển hoá năng lượng
-
Công của nguồn điện sản ra trong thời gian t:
\(A{\rm{ }} = {\rm{ }}E.It\) (3)
-
Nhiệt lượng toả ra trên toàn mạch :
\(Q = ({R_N} + {\rm{ }}r){I^2}t\) (4)
-
Theo định luật bảo toàn năng lượng thì A = Q.
-
Ta có: \({\mathop{\rm I}\nolimits} = \frac{E}{{{R_N} + r}}\)
-
Như vậy định luật Ôm đối với toàn mạch hoàn toàn phù hợp với định luật bảo toàn và chuyển hoá năng lượng.
3.3. Hiệu suất nguồn điện
\(H = \frac{{{A_{cx}}}}{A}\frac{{{U_N}.It}}{{{\rm{E}}It}} = \frac{{{U_N}}}{{\rm{E}}}\)
-
Vận dụng: Nếu mạch ngoài chỉ có điện trở RN:
\(H = \frac{{{R_N}}}{{{R_N} + r}}\)
Bài 1:
Nhận xét nào sau đây đúng? Theo định luật Ôm cho toàn mạch thì cường độ dòng điện cho toàn mạch:
A. Tỉ lệ nghịch với suất điện động của nguồn.
B. Tỉ lệ nghịch điện trở trong của nguồn.
C. Tỉ lệ nghịch với điện trở ngoài của nguồn.
D. Tỉ lệ nghịch với tổng điện trở trong và điện trở ngoài.
Hướng dẫn giải
Chọn đáp án D
-
Tỉ lệ nghịch với tổng điện trở trong và điện trở ngoài.
\({\mathop{\rm I}\nolimits} = \frac{E}{{{R_N} + r}}\)
Bài 2:
Đối với mạch điện kín gồm nguồn điện với mạch ngoài là điện trở thì cường độ dòng điện chạy trong mạch:
A. Tỷ lệ thuận với điện trở mạch ngoài
B. Giảm khi điện trở mạch ngoài tăng.
C. Tỷ lệ nghịch với điện trở mạch ngoài
D. Tăng khi điện trở mạch ngoài tăng.
Hướng dẫn giải
Chọn đáp án B
-
Giảm khi điện trở mạch ngoài tăng
Bài 3:
Mắc một điện trở 14\(\Omega \) vào hai cực của nguồn điện có điện trở trong r=1\(\Omega \) thì hiệu điện thế giữa hai cực của nguồn điện là 8,4V.
Tính cường độ dòng điện chạy trong mạch ?
Hướng dẫn giải:
Ta có:
\(\begin{array}{l}
{\rm{I}} = \frac{E}{{{{\rm{R}}_{{\rm{td}}}} + {\rm{r}}}}\\
= \frac{{\rm{2}}}{{({\rm{5}},{\rm{5}} + {\rm{4}},{\rm{4}}) + {\rm{0}},{\rm{1}}}} = {\rm{0}},{\rm{2A}}
\end{array}\)
Bài 4:
Xét mạch điện kín gồm nguồn điện có suất điện động E = 2V, điện trở trong r = 0,1 \(\Omega \) mắc với điện trở ngoài R = 100 \(\Omega \). Tìm hiệu điện thế giữa 2 cực của nguồn điện.
Hướng dẫn giải:
Ta có:
\(I = \frac{E}{{R + r}} = \frac{2}{{100 + 0,1}} = \frac{2}{{100,1}}(A)\)
\(U = {\rm{IR}} = \frac{2}{{100,1}}.100 = \frac{{200}}{{100,1}} = 1,998V\)
Bài 5:
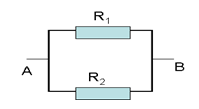
Cho mạch điện như hình vẽ
\({R_1} = {\rm{ }}20W{\rm{ }};{\rm{ }}{R_2} = {\rm{ }}20W{\rm{ }},{\rm{ }}{U_{AB}} = {\rm{ }}60V.\) Tính:
a) Tính điện trở của đoạn mạch?
b) Cường độ dòng qua đoạn mạch?
c) Cường độ dòng điện qua mỗi điện trở và Hiệu điện thế hai đầu mỗi điện trở?
d) Tính công và công suất mà đoạn mạch tiêu thụ trong 1giờ.
Hướng dẫn giải:
a. Vì mạch điện mắc song song nên ta có:
\(\begin{array}{l}
{R_1}//{R_2}\\
\Rightarrow {R_{AB}} = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = 10\Omega
\end{array}\)
b. Cường độ dòng qua đoạn mạch:
\(I = \frac{{{U_{AB}}}}{{{R_{AB}}}} = 6A\)
c. Cường độ dòng điện và Hiệu điện thế hai đầu của mỗi điện trở:
\(\begin{array}{l}
{I_1} = {\rm{ }}{I_2} = 3A\\
{U_1} = {U_2} = U = 60V
\end{array}\)
d. Công và công suất mà đoạn mạch:
\(\begin{array}{*{20}{l}}
{A{\rm{ }} = {\rm{ }}UIt{\rm{ }} = 60.6.3600 = 1296000J}\\
{P{\rm{ }} = {\rm{ }}UI{\rm{ }} = 360W}
\end{array}\)
1. Thí nghiệm
-
Toàn mạch là một mạch điện kín gồm: Nguồn điện (E,r) nối với mạch ngoài là các vật dẫn có điện trở tương đương R
-
Mắc mạch điện như hình vẽ:
Thiết lập định luật Ôm cho toàn mạch
-
Nguồn điện thực hiện 1 công \( A = EIt\).
-
Nhiệt lượng tỏa ra ở điện trở ngoài và điện trở trong của nguồn điện:
\(Q = R{I^2}t + r{I^2}t.\)
-
Theo Định luật bảo toàn và chuyển hóa năng lượng:
\(Q= A\) hay \(R{I^2}.t + {\rm{ }}r{I^2}.t = EIt\)
\(\begin{array}{l}
\Rightarrow E = RI + rI = I(R + r)\\
\Rightarrow I = \frac{E}{{R + r}}
\end{array}\)
-
Dùng thí nghiệm chứng minh để thiết lập biểu thức định luật Ôm cho toàn mạch
.PNG)
\({U_{AB}} = E - Ir\)
2. Định luật Ôm đối với toàn mạch
2.1. Biểu thức:
\({\mathop{\rm I}\nolimits} = \frac{E}{{{R_N} + r}}\) (1)
2.2. Phát biểu:
-
Cường độ dòng điện chạy trong mạch điện kín tỉ lệ thuận với suất điện động của nguồn điện và tỉ lệ nghịch với điện trở toàn phần của mạch đó.
-
Lưu ý:
\(\begin{array}{l}
{\rm{I}} = \frac{E}{{{R_N} + r}}\\
\Leftrightarrow E = {\rm{I}}({R_N} + r)\\
\Rightarrow E = {{\rm{U}}_N} + Ir
\end{array}\)
\(E = {U_N}\) Khi: r = 0 hoặc mạch hở (I = 0)
3. Nhận xét
3.1. Hiện tượng đoản mạch
-
Là hiện tượng nối tắt 2 cực của nguồn bằng dây dẫn có điện trở rất nhỏ.
-
Cường độ dòng điện trong mạch kín đạt giá trị lớn nhất khi \({R_N} = 0\) . Khi đó ta nói rằng nguồn điện bị đoản mạch.
\(I = \frac{E}{r}\) (2)
-
Khi đó: \(R \approx 0\) và \({I_{m{\rm{ax}}}} = \frac{E}{r}\)
-
Tác hại của hiện tượng đoản mạch là gây lên cháy chập mạch điện, đó chính là một trong những nguyên nhân dẫn tới các vụ cháy .
3.2. Định luật Ôm đối với toàn mạch và định luật bảo toàn và chuyển hoá năng lượng
-
Công của nguồn điện sản ra trong thời gian t:
\(A{\rm{ }} = {\rm{ }}E.It\) (3)
-
Nhiệt lượng toả ra trên toàn mạch :
\(Q = ({R_N} + {\rm{ }}r){I^2}t\) (4)
-
Theo định luật bảo toàn năng lượng thì A = Q.
-
Ta có: \({\mathop{\rm I}\nolimits} = \frac{E}{{{R_N} + r}}\)
-
Như vậy định luật Ôm đối với toàn mạch hoàn toàn phù hợp với định luật bảo toàn và chuyển hoá năng lượng.
3.3. Hiệu suất nguồn điện
\(H = \frac{{{A_{cx}}}}{A}\frac{{{U_N}.It}}{{{\rm{E}}It}} = \frac{{{U_N}}}{{\rm{E}}}\)
-
Vận dụng: Nếu mạch ngoài chỉ có điện trở RN:
\(H = \frac{{{R_N}}}{{{R_N} + r}}\)
Bài 1:
Nhận xét nào sau đây đúng? Theo định luật Ôm cho toàn mạch thì cường độ dòng điện cho toàn mạch:
A. Tỉ lệ nghịch với suất điện động của nguồn.
B. Tỉ lệ nghịch điện trở trong của nguồn.
C. Tỉ lệ nghịch với điện trở ngoài của nguồn.
D. Tỉ lệ nghịch với tổng điện trở trong và điện trở ngoài.
Hướng dẫn giải
Chọn đáp án D
-
Tỉ lệ nghịch với tổng điện trở trong và điện trở ngoài.
\({\mathop{\rm I}\nolimits} = \frac{E}{{{R_N} + r}}\)
Bài 2:
Đối với mạch điện kín gồm nguồn điện với mạch ngoài là điện trở thì cường độ dòng điện chạy trong mạch:
A. Tỷ lệ thuận với điện trở mạch ngoài
B. Giảm khi điện trở mạch ngoài tăng.
C. Tỷ lệ nghịch với điện trở mạch ngoài
D. Tăng khi điện trở mạch ngoài tăng.
Hướng dẫn giải
Chọn đáp án B
-
Giảm khi điện trở mạch ngoài tăng
Bài 3:
Mắc một điện trở 14\(\Omega \) vào hai cực của nguồn điện có điện trở trong r=1\(\Omega \) thì hiệu điện thế giữa hai cực của nguồn điện là 8,4V.
Tính cường độ dòng điện chạy trong mạch ?
Hướng dẫn giải:
Ta có:
\(\begin{array}{l}
{\rm{I}} = \frac{E}{{{{\rm{R}}_{{\rm{td}}}} + {\rm{r}}}}\\
= \frac{{\rm{2}}}{{({\rm{5}},{\rm{5}} + {\rm{4}},{\rm{4}}) + {\rm{0}},{\rm{1}}}} = {\rm{0}},{\rm{2A}}
\end{array}\)
Bài 4:
Xét mạch điện kín gồm nguồn điện có suất điện động E = 2V, điện trở trong r = 0,1 \(\Omega \) mắc với điện trở ngoài R = 100 \(\Omega \). Tìm hiệu điện thế giữa 2 cực của nguồn điện.
Hướng dẫn giải:
Ta có:
\(I = \frac{E}{{R + r}} = \frac{2}{{100 + 0,1}} = \frac{2}{{100,1}}(A)\)
\(U = {\rm{IR}} = \frac{2}{{100,1}}.100 = \frac{{200}}{{100,1}} = 1,998V\)
Bài 5:
Cho mạch điện như hình vẽ
\({R_1} = {\rm{ }}20W{\rm{ }};{\rm{ }}{R_2} = {\rm{ }}20W{\rm{ }},{\rm{ }}{U_{AB}} = {\rm{ }}60V.\) Tính:
a) Tính điện trở của đoạn mạch?
b) Cường độ dòng qua đoạn mạch?
c) Cường độ dòng điện qua mỗi điện trở và Hiệu điện thế hai đầu mỗi điện trở?
d) Tính công và công suất mà đoạn mạch tiêu thụ trong 1giờ.
Hướng dẫn giải:
a. Vì mạch điện mắc song song nên ta có:
\(\begin{array}{l}
{R_1}//{R_2}\\
\Rightarrow {R_{AB}} = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = 10\Omega
\end{array}\)
b. Cường độ dòng qua đoạn mạch:
\(I = \frac{{{U_{AB}}}}{{{R_{AB}}}} = 6A\)
c. Cường độ dòng điện và Hiệu điện thế hai đầu của mỗi điện trở:
\(\begin{array}{l}
{I_1} = {\rm{ }}{I_2} = 3A\\
{U_1} = {U_2} = U = 60V
\end{array}\)
d. Công và công suất mà đoạn mạch:
\(\begin{array}{*{20}{l}}
{A{\rm{ }} = {\rm{ }}UIt{\rm{ }} = 60.6.3600 = 1296000J}\\
{P{\rm{ }} = {\rm{ }}UI{\rm{ }} = 360W}
\end{array}\)
.PNG)
.PNG)