Tài liệu ôn thi vào lớp 10 môn Toán
Tài liệu ôn thi vào lớp 10 môn Toán: Đồ thị bậc 2 - Tương giao bậc 1 và 2 là tài liệu ôn thi vào lớp 10 tham khảo cho các em học sinh lớp 9. Tài liệu học tập này môn Toán do thầy Nguyễn Chí Thành biên soạn, dành cho các bạn học sinh lớp 9 nghiên cứu, hệ thống củng cố kiến thức Toán 9 cũng như luyện đề, bài tập nhằm có các cách giải toán được nhanh nhất, thông minh nhất, giúp các bạn ôn thi môn Toán vào lớp 10 được hiệu quả cao.
Tài liệu ôn thi vào lớp 10 môn Toán
Tài liệu ôn thi vào lớp 10 môn toán chi tiết và đầy đủ các dạng bài tập
HÀM SỐ y=ax2(a≠0)
Dạng 1: Tìm m để A(x0; y0) nằm trên đồ thị
Phương pháp: Thay x =x0; y= y0 vào đồ thị để tìm m.
BÀI TẬP:
Bài 1: Cho y = mx2.
a) Tìm m biết đồ thị qua C(2;8).
b) Biết điểm A(2;b) thuộc đồ thị, hỏi điểm B(-2;b) có thuộc đồ thị không? vì sao?
c) Biết D(a;-4) thuộc đồ thị, hỏi điểm E(a;4) có thuộc đồ thị không? vì sao?
HD:
a) Vì đồ thị qua C(2;8) nên thay x=2; y=8 vào đồ thị ta được: 8=m.4 ↔m=2. Vậy y=2x2.
b) Vì điểm A(2;b) thuộc đồ thị nên b=m.22 hay b=4m (1)
Thay tọa độ điểm B(-2;b) vào đồ thị ta được: b =m(-2)2 hay b =4m (2)
Từ (1)(2) suy ra B(-2;b) thuộc đồ thị.
c) Thay D(a;-4) vào đồ thị ta được: -4 = ma2.
Thay E(a;4) vào đồ thị ta được: 4 =ma2. Suy ra E không thuộc đồ thị.
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến, đạt GTLN, GTNN bằng 0. Phương pháp:
- Nếu a > 0 thì hàm số nghịch biến khi x< 0 và đồng biến khi x> 0.
- Nếu a < 0 thì hàm số đồng biến khi x< 0 và nghịch biến khi x> 0.
- Hàm số đạt GTNN bằng 0 khi a> 0.
- Hàm số đạt GTLN bằng 0 khi a< 0.
BÀI TẬP:
Bài 1: Cho y =(m-1)x2.
a) Tìm m để hàm số đồng biến với x> 0.
b) Tìm m để hàm số nghịch biến với x< 0.
c) Hàm số nghịch biến với x> 0.
HD:
a) Hàm số đồng biến với x> 0 khi m-1> 0↔ m> 1.
b) Hàm số nghịch biến với x< 0 khi m-1> 0 ↔m> 1.
c) Hàm số nghịch biến với x> 0 khi m-1< 0 ↔m< 1.
Bài 2: Cho y=(m2-m)x2. Tìm m để:
a) Hàm số đạt GTNN bằng 0.
b) Hàm số đạt GTLN bằng 0.
HD:
a) Hàm số đạt GTNN bằng 0 khi m2–m > 0 ↔m(m-1) > 0↔ m > 1 hoặc m < 0.
b) Hàm số đạt GTLN bằng 0 khi m2–m < 0 ↔0 < m < 1.
Dạng 3: Vẽ đồ thị hàm số y= ax2 (a≠0).
Phương pháp: Đồ thị hàm số nhận Oy làm trục đối xứng, Các em kẻ bảng các giá trị tương ứng x, y, tìm 5 điểm đồ thị đi qua rồi vẽ.
BÀI TẬP:
Bài 1: Vẽ đồ thị hàm số y = x2. Đồ thị nhận Oy làm trục đối xứng.
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
- Vẽ đồ thị:
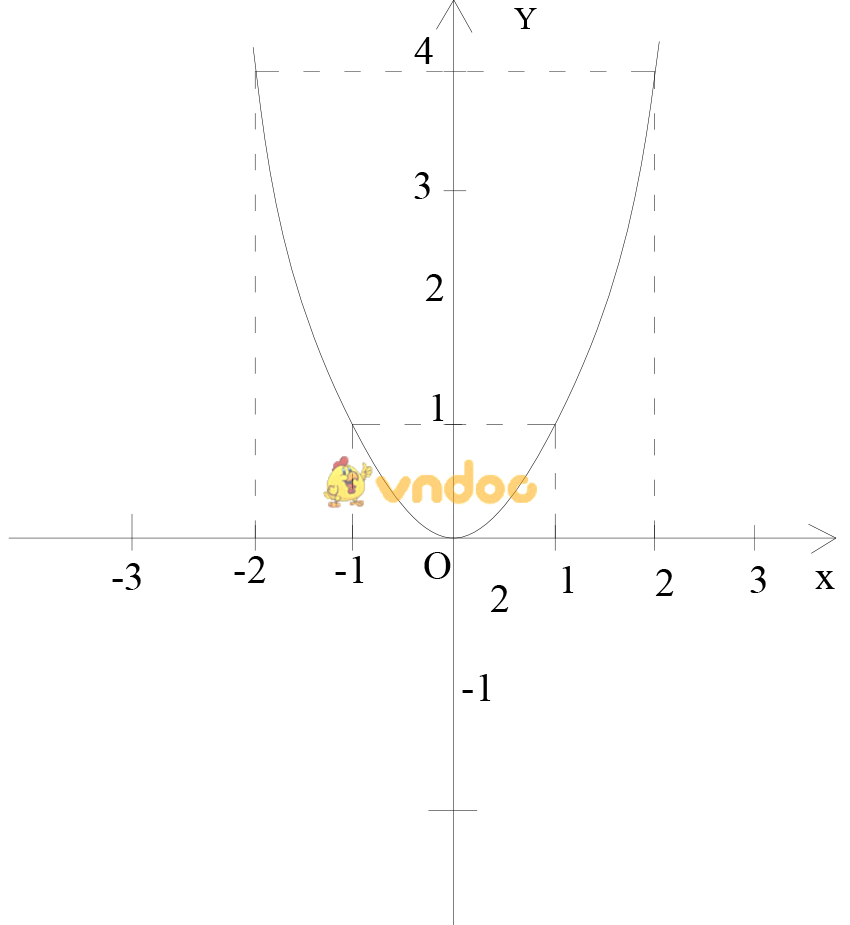
Dạng 4: Tìm m để hai đồ thi y=f(x)=mx+n và y=g(x)=ax2+bx+c tiếp xúc nhau:
Phương pháp:
- Xét giao điểm của 2 đồ thị thỏa mãn phương trình: f(x)=g(x).
- Đưa phương trình về dạng: Ax2 +Bx+C=0 (1).
- Để hai đồ thị tiếp xúc nhau thì phương trình (1) phải có nghiệm kép:
| { | ≠0 | Từ đó tìm được m |
| Δ=B2 - 4AC = 0 |
BÀI TẬP:
Bài 1: Cho Parabol (P) y = ax2 tiếp xúc với đường thẳng (d): y = x - 1
a. Xác định hệ số a
b. Tìm toạ độ tiếp điểm của (d) và (P)

Toạ độ tiếp điểm là: (2; 1)
Bài 5: Cho Parabol: y=x2. Xác định hệ số n để đường thẳng: y=2x+n tiếp xúc với
(P). Tìm toạ độ tiếp điểm
Giải
- Phương trình hoành độ điểm chung của (P) và (d ) là:
x2-2x-n=0. Ta có: Δ'= 1 + n.
Vì (P) và (d) tiếp xúc → Δ'= 0 → 1 + n = 0 → n = -1
- Lúc đó phương trình đường thẳng là: y=2x-1
- Phương trình hoành độ điểm chung là: x2-2x+1=0
- Giải phương trình được: x1=x2=1
→ y=12=1
Toạ độ tiếp điểm là: (1; 1)
Bài 6: Cho (P): y = x2 lập phương trình đường thẳng (d) song song với đường thẳng (d1): y = 2x và tiếp xúc với (P).
Giải
- Phương trình có dạng: y=ax+b
- Vì (d) song song d1 → a=2
- Vì (d) tiếp xúc (P) → Phương trình hoành độ điểm chung của (d) và (P) là:
x2-2x-b = 0. Ta có: Δ'=1+b
- Vì tiếp xúc → Δ'=0 →b = -1







