Dưới đây là một số đề thi được chúng tôi giới thiệu tới bạn đọc. Quý bạn đọc có thể tải file để xem chi tiết tất cả các môn.

Đề thi học sinh giỏi môn Toán và Văn:

ĐỀ THI MÔN: TOÁN

Bài 1: (7,0 điểm)

1. Hàm số y = f(x) xác định và có đạo hàm trên tập số thực, thỏa điều kiện: [f(1 + 2x)]² = x - [f(1 - x)]³, với mọi x thuộc R. Hãy viết phương trình tiếp tuyến với đồ thị hàm số y = f(x) tại điểm có hoành độ x = 1.

2. Cho hai hàm số: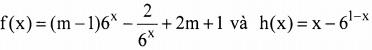
Tìm m để f(x).h(x) ≥ 0 với mọi x thuộc [0; 1]

Bài 2: (6,0 điểm)

1. Giải phương trình:

2. Cho tập hợp A = {0; 4; 5; 6; 7; 8}. Hỏi có thể lập được bao nhiêu số có 4 chữ số (các chữ số này chọn từ tập A) sao cho mỗi số tạo thành đều chia hết cho 4?

Bài 3: (7,0 điểm)

1. Cho lục giác lồi ABCDEF thỏa mãn: AB = BC; CD = DE; EF = FA. Tìm giá trị nhỏ nhất của biểu thức:
. Khi đó có nhận xét gì về hình tính lục giác ABCDEF?

2. Trong mặt phẳng tọa độ Oxy, cho (P_m) là đồ thị của hàm số: y = 5x² + mx - (23m² + 10m + 2012)

Gọi (C_m) là đường tròn đi qua 3 giao điểm của (P_m) với các trục tọa độ. Chứng minh rằng khi m thay đổi các đường tròn (C_m) luôn đi qua 1 điểm cố định.

ĐỀ THI MÔN: NGỮ VĂN

Câu 1: (8,0 điểm)

Bàn về vai trò của kết quả trong cuộc sống của con người, có ý kiến cho rằng: "Vinh quang nằm trong nỗ lực, không phải kết quả, nỗ lực hết mình là thắng lợi hoàn toàn". (Mahatma Gandhi - Ấn Độ).

Nhưng cũng có người cho rằng: "Anh không thể nói anh hạnh phúc nếu anh không thắng cuộc". (Arsene Wenger - Pháp)

Anh/chị có suy nghĩ gì về hai ý kiến trên?

Câu 2: (12 điểm)

Trong quyển lý luận văn học - Vấn đề và suy nghĩ (NXBGD, 1988, trang 23) Giáo sư Nguyễn Văn Hạnh đã nhận xét:

"... sáng tác văn chương nghệ thuật là do một sự thôi thúc từ bên trong, do muốn trình bày những ấn tượng mới mẻ, độc đáo, đầy ắp trong con người mình. Người nghệ sĩ luôn cảm thấy qua tác phẩm mình sẽ nói một điều chưa ai nói, hoặc chưa ai nói như mình"

Anh/chị hiểu như thế nào về nhận xét trên? Bằng thực tế cảm nhận tác phẩm văn học của mình, anh/chị hãy làm sáng tỏ ý kiến trên.