Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi học sinh giỏi lớp 12 THPT tỉnh Lâm Đồng năm 2013 - 2014.

Đề thi học sinh giỏi môn Toán:

Bài 1:

Giải hệ phương trình: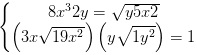

Bài 2:

Cho a, b, c là 3 số thực dương thỏa abc = 1. Tìm giá trị nhỏ nhất của biểu thức:

Bài 3:

1) Cho hai đường tròn (O₁) và (O₂) lần lượt có bán kính là R₁, R₂ (R₁ < R₂) tiếp xúc trong tại A. Gọi M là điểm di động trên (O₁) (M khác A), tiếp tuyến của (O₁) tại M cắt (O₂) tại B và C. Gọi M’ (M’ khác A) là giao điểm của AM với (O₂)

a) Chứng minh AM’ là đường phân giác của góc ABC.

b) Tìm quỹ tích tâm I của đường tròn nội tiếp tam giác ABC.

2) Cho đường tròn (C) có tâm I và đường kính AB, trên đoạn IB lấy điểm C (C khác I và B). Đường thẳng (d) vuông góc với AB tại C và H là điểm thay đổi trên (d). Đường thẳng AH cắt đường tròn (C) tại điểm D và đường tròn BH cắt đường tròn (C) tại E. Chứng minh đường thẳng DE luôn đi qua điểm cố định.

Bài 4: Cho dãy số (x_n), n = 1, 2, 3,.. xác định bởi

a) Chứng minh:

b) Tìm:

Bài 5: Tìm tất cả hàm số liên tục f: R → R sao cho: f(x)f(x⁴) = 4026xx⁴