Toán lớp 4 trang 87 - Bài 63: Phép nhân phân số - SGK Kết nối tri thức

Câu 1

Tính.

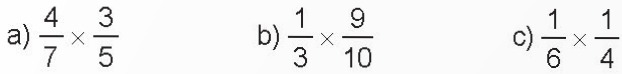
Phương pháp giải:

 Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

Lời giải chi tiết:

a) \({\text{}}\;\frac{4}{7} \times \frac{3}{5} = \frac{{4 \times 3}}{{7 \times 5}} = \frac{{12}}{{35}}\)

b) \(\;\frac{1}{3} \times \frac{9}{{10}} = \frac{{1 \times 9}}{{3 \times 10}} = \frac{9}{{30}} = \frac{3}{{10}}\)

c) \(\;\frac{1}{6} \times \frac{1}{4} = \frac{{1 \times 1}}{{6 \times 4}} = \frac{1}{{24}}\)

Câu 2

Rút gọn rồi tính.

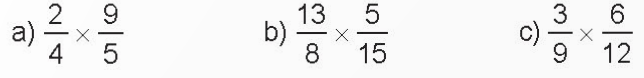
Phương pháp giải:

Rút gọn các phân số chưa tối giản rồi thực hiện nhân hai phân số 

Lời giải chi tiết:

a) \(\;\frac{2}{4} \times \frac{9}{5} = \;\frac{1}{2} \times \frac{9}{5} = \frac{{1 \times 9}}{{2 \times 5}} = \frac{9}{{10}}\)

b) \(\frac{{13}}{8} \times \frac{5}{{15}} = \frac{{13}}{8} \times \frac{1}{3} = \frac{{13 \times 1}}{{8 \times 3}} = \frac{{13}}{{24}}\)

c) \(\;\;\frac{3}{9} \times \frac{6}{{12}} = \frac{1}{3} \times \frac{1}{2} = \frac{{1 \times 1}}{{3 \times 2}} = \frac{1}{6}\)

Câu 3

Tìm phân số thích hợp.

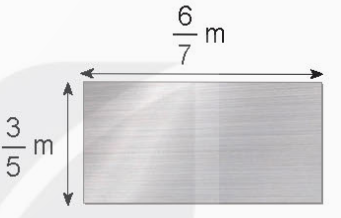
Một tấm nhôm hình chữ nhật (như hình vẽ) có chiều dài ? m và chiều rộng ? m.

Diện tích tấm nhôm đó là ? m²

Phương pháp giải:

- Quan sát hình vẽ để xác định chiều dài, chiều rộng của tấm nhôm

- Để tìm diện tích tấm nhôm, ta lấy chiều dài nhân chiều rộng.

Lời giải chi tiết:

Một tấm nhôm hình chữ nhật (như hình vẽ) có chiều dài là $\frac{6}{7}$m và chiều rộng $\frac{3}{5}$m.

Diện tích tấm nhôm đó là: $\frac{6}{7} \times \frac{3}{5} = \frac{{18}}{{35}}$ m²

Câu 1

Tính (theo mẫu).

Phương pháp giải:

Muốn nhân một phân số với số tự nhiên ta có thể lấy tử số nhân với số tự nhiên và giữ nguyên mẫu số.

Lời giải chi tiết:

a) \(\frac{9}{{11}} \times 8 = \frac{{9 \times 8}}{{11}} = \frac{{72}}{{11}}\)

b) \(\;\frac{4}{5} \times 1 = \frac{{4 \times 1}}{5} = \frac{4}{5}\)

c) \(\frac{{15}}{8} \times 0 = \frac{{15 \times 0}}{8} = 0\)

Câu 2

Tính (theo mẫu).

Phương pháp giải:

Muốn nhân một số tự nhiên với phân số ta có thể lấy số tự nhiên nhân với tử số và giữ nguyên mẫu số.

Lời giải chi tiết:

a) \({\text{}}\;3 \times \frac{4}{{11}} = \frac{{3 \times 4}}{{11}} = \frac{{12}}{{11}}\)

b) \(\;1 \times \frac{5}{4} = \frac{{1 \times 5}}{4} = \frac{5}{4}\)

c) \(0 \times \frac{2}{5} = \frac{{0 \times 2}}{5} = 0\)

Câu 3

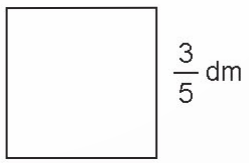
Tình chu vi hình vuông có cạnh $\frac{3}{5}$dm.

Phương pháp giải:

Chu vi hình vuông = độ dài cạnh hình vuông x 4.

Lời giải chi tiết:

Chu vi hình vuông là:

$\frac{3}{5} \times 4 = \frac{{12}}{5}({\text{dm}})$

Đáp số: $\frac{{12}}{5}{\text{dm}}$

Câu 4

Một tàu vũ trụ bay vòng quanh một thiên thể 6 vòng rồi mới đáp xuống. Nếu mỗi vòng tàu vũ trụ bay được $\frac{{61}}{6}$ km thì nó đã bay tất cả bao nhiêu ki-lô-mét quanh thiên thể?

Phương pháp giải:

Số km tàu vũ trụ đã bay quanh thiên thể = số km bay trong mỗi vòng x số vòng.

Lời giải chi tiết:

Tóm tắt:

Mỗi vòng: $\frac{{61}}{6}$ km

6 vòng: ? km

Bài giải

Số km tàu vũ trụ đã bay quanh thiên thể là:

$\frac{{61}}{6} \times 6 = 61\,\,({\text{km}})$

Đáp số: 61 km

Câu 1

>, <, = ?

Phương pháp giải:

Áp dụng các tính chất giao hoán, kết hợp, nhân một tổng với một số để so sánh các biểu thức đã cho.

Lời giải chi tiết:

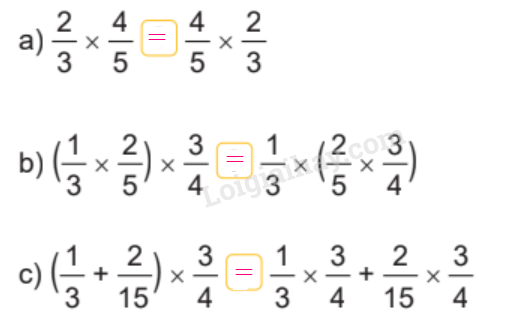
Câu 2

Tính.

Phương pháp giải:

a) Áp dụng tính chất giao hoán, kết hợp của phép nhân

b) Với biểu thức có chứa dấu ngoặc ta thực hiện phép tính ở trong ngoặc trước

Lời giải chi tiết:

a) \(\frac{3}{{22}} \times \frac{3}{{11}} \times {\text{22}}\)

$ = (\frac{3}{{22}} \times 22) \times \frac{3}{{11}}$

$ = 3 \times \frac{3}{{11}}$

$ = \frac{9}{{11}}$

b) \(\;\left( {\frac{1}{3} + \frac{1}{6}} \right) \times \frac{2}{5}\)

$ = \frac{1}{2} \times \frac{2}{5}$

$ = \frac{1}{5}$

Câu 3

Một bè nuôi cá tra hình chữ nhật có chiều dài $\frac{{25}}{2}$m, chiều rộng $\frac{{19}}{2}$m. Hỏi chu vi của bè cá đó là bao nhiêu mét?

Phương pháp giải:

Chu vi bè cá hình chữ nhật = (chiều dài + chiều rộng) x 2

Lời giải chi tiết:

Tóm tắt

Bè nuôi cá hình chữ nhật

Chiều dài: $\frac{{25}}{2}$m

Chiều rộng: $\frac{{19}}{2}$m

Chu vi: ? m

Bài giải

Chu vi của bè cá đó là:

$\left( {\frac{{25}}{2} + \frac{{19}}{2}} \right) \times 2 = 44\,\,{\text{(m)}}$

Đáp số: 44 m

Câu 4

Số?

Nhà cô Sáu có 2 chuồng lợn, mỗi chuồng nuôi 4 con lợn. Mỗi ngày, một con lợn ăn hết $\frac{1}{8}$ yến cám. Mỗi ngày các con lợn nhà cô Sáu ăn hết bao nhiêu kg cám?

Phương pháp giải:

Bước 1: Số con lợn nhà cô Sáu = số con lợn trong một chuồng x số chuồng.

Bước 2: Số kg cám các con lợn nhà cô Sáu ăn = số kg cám 1 con lợn ăn x số con lợn

              Đổi đơn vị từ yến về kg

Lời giải chi tiết:

Tóm tắt

Có: 2 chuồng

Mỗi chuồng: 4 con

1 con: $\frac{1}{8}$ yến cám

Tất cả: ? kg cám

Bài giải

Nhà cô Sáu có số con lợn là:

4 x 2 = 8 (con lợn)

Số ki-lô-gam cám mỗi ngày các con lợn nhà cô Sáu ăn là:

$\frac{1}{8} \times 8 = 1\,\,$(yến) = 10 kg

Đáp số: 10 kg cám

Câu 5

Đ, S?

Có ba đoạn tre A, B, C xếp như hình vẽ. Biết đoạn tre A dài 1m và có 3 đốt dài bằng nhau, đoạn tre C có 2 đốt dài bằng nhau.

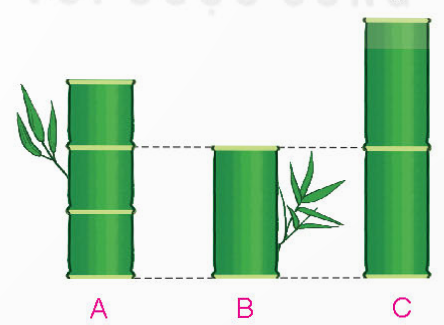
a) Đoạn tre B có độ dài là $\frac{2}{3}$ m    …….

b) Đoạn tre dài nhất có độ dài là $\frac{3}{2}$ m  …….

Phương pháp giải:

Quan sát hình vẽ để tìm độ dài mỗi đoạn tre, nếu đúng ghi Đ, sai ghi S.

Lời giải chi tiết:

Ta thấy: Đoạn tre B có độ dài bằng $\frac{2}{3}$ đoạn tre A và bằng $\frac{2}{3}$m.

Đoạn tre C dài gấp 2 lần đoạn tre B nên độ dài đoạn tre C là: $\frac{2}{3} \times 2 = \frac{4}{3}$ (m)

Vậy ta có kết quả như sau:

a) Đoạn tre B có độ dài là $\frac{2}{3}$ m             Đ

b) Đoạn tre dài nhất có độ dài là $\frac{3}{2}$ m   S

Câu 1

Tính rồi rút gọn.

Phương pháp giải:

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số

- Rút gọn các kết quả chưa tối giản.

Lời giải chi tiết:

a) \(\,\frac{5}{{11}} \times \frac{{11}}{6} = \frac{{5 \times 11}}{{11 \times 6}} = \frac{{55}}{{66}} = \frac{5}{6}\,\,\)

b) \(7 \times \frac{6}{{21}} = \frac{{7 \times 6}}{{21}} = \frac{{42}}{{21}} = 2\)

Câu 2

Tính bằng cách thuận tiện.

Phương pháp giải:

Áp dụng công thức:

a x b + a x c = a x (b + c)

Lời giải chi tiết:

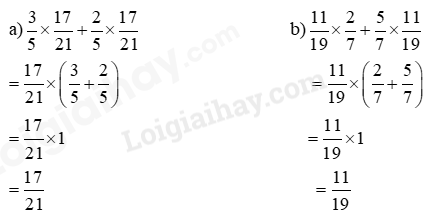
Câu 3

Tìm phân số thích hợp.

Mỗi ô đỗ xe ô tô có dạng hình chữ nhật với chiều dài $\frac{{11}}{2}$m và chiều rộng $\frac{5}{2}$m

a) Diện tích mỗi ô đỗ xe đó là ..?.. m²

b) Tổng diện tích của 3 ô đỗ xe ..?.. m²

Phương pháp giải:

- Diện tích mỗi ô đỗ xe = chiều dài x chiều rộng

- Tổng diện tích của 3 ô đỗ xe = diện tích mỗi ô đỗ xe x 3

Lời giải chi tiết:

a) Diện tích mỗi ô đỗ xe đó là $\frac{{11}}{2} \times \frac{5}{2} = \frac{{55}}{4}$ (m²)

b) Tổng diện tích của 3 ô đỗ xe $\frac{{55}}{4} \times 3 = \frac{{165}}{4}$ (m²)

Câu 4

Trong bữa tiệc, nhà vua chia bánh cho 8 hiệp sĩ. Mỗi hiệp sĩ được chia nửa cái bánh pi-da bò và $\frac{1}{8}$ bánh pi-da gà. Hỏi 8 hiệp sĩ được chia tất cả bao nhiêu cái bánh?

Phương pháp giải:

- Tính số bánh của 1 hiệp sĩ được chia.

- Tính số bánh của 8 hiệp sĩ được chia.

Lời giải chi tiết:

Mỗi hiệp sĩ được chia nửa cái bánh pi-da bò tức là mỗi hiệp sĩ được chia $\frac{1}{2}$ cái bánh pi-da bò.

Mỗi hiệp sĩ được chia số cái bánh là:

            $\frac{1}{2} + \frac{1}{8} = \frac{5}{8}$(cái bánh)

8 hiệp sĩ được chia tất cả số cái bánh là:

             $\frac{5}{8} \times 8 = 5$ (cái bánh)

                Đáp số: 5 cái bánh

Câu 5

Tìm phân số thích hợp.

Nhà vua đố trạng Hiền tính được diện tích phần màu xanh trong hình bên. Biết diện tích hình tam giác ABC bằng diện

tích hình tam giác CDE và độ dài cạnh của mỗi hình vuông nhỏ là $\frac{8}{5}$ dm. Diện tích phần màu xanh là ..?.. dm²

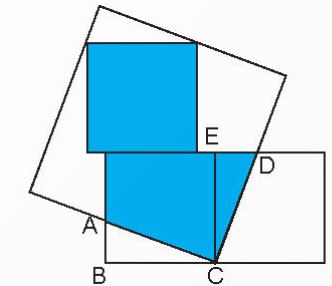
Phương pháp giải:

Diện tích hình vuông = cạnh x cạnh

Diện tích phần màu xanh = diện tích hình vuông x 2

Lời giải chi tiết:

Diện tích hình vuông màu xanh là: $\frac{8}{5} \times \frac{8}{5} = \frac{{64}}{{25}}$ (dm²)

Diện tích phần màu xanh bằng 2 lần diện tích của hình vuông màu xanh.

Diện tích phần màu xanh là $\frac{{64}}{{25}} \times 2 = \frac{{128}}{{25}}$ (dm²)

Vậy phân số cần điền là $\frac{{128}}{{25}}$